2017-2018 ACM-ICPC Latin American Regional Programming Contest
ECNU Foreigners
Problem A
Solved by kblack. 03:24 (+2)
题意:一堆高度相同(有固定平行边)的凸多边形,要求找到最好的顺序把所有多边形卡在一起最短。
题解:枚举多边形对,从下到上判断边对之间卡在一起的距离,然后状压 DP 求最短的排列,搞一个 (0, 0) 到 (0, H) 的“多边形”后面写起来会方便点。
Problem B
Solved by kblack. 00:54 (+)
题意:一个 CodeBlocks,输入元音会导致已经输入的倒置,求输入指定串的方案数。
题解:发现多余一个元音的时候上一个输入的字符都是唯一的,只有最初的元音后面的辅音是可以有多解的,找到就好。
Problem D
Solved by zerol & ultmaster. 02:00 (+)
题意:数列染色,强制在线,支持区间染色和询问某种颜色的数量。
题解:由于颜色数众多,所以没法线段树。用 set 维护所有不相交区间的端点和颜色,同时数组维护每种颜色的出现次数,每次询问至多增加一个区间,对于与之相交的区间,进行删除或者切分。这题还可以分块做。
Problem D
Solved by zerol. 02:00 (+)
Problem E
Solved by ultmaster. 01:24 (+)
Problem F
Solved by ultmaster. 00:29 (+1)
Problem G
Solved by zerol. 02:15 (+)
题解:有树形的与非门组成的电路,有些门坏了,会一直输出 0 或 1,求有多少种不同的输入能使输出结果错误。
题解:树形 dp。状态 2×2,表示预测值和实际值分别为 0 或 1 的情况。
Problem H
Solved by kblack. 00:08 (+)
温暖的签到。
Problem I
Solved by zerol. 01:13 (+)
题意:询问强制选取某个边的最小生成树的值。
题解:经典题。建最小生成树,对于询问的边,答案就是 最小生成树的权 - 这条路径上权最大的边 + 这条边的权。用树上倍增维护会比较好写。
Problem J
Solved by ultmaster. 00:44 (+)
Problem K
Solved by kblack. 04:23 (+2)
题意:一个矩阵,四种图形,问能否用指定方式铺满。
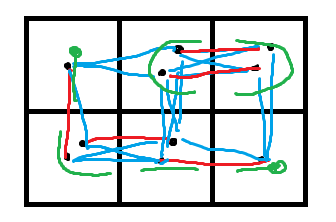
题解:图形 $1$ 相当于他和四周有一个连接,图形 $2, 3, 4$ 相当于他和四周有两个连接,拆分成对应数量的点,和周围连边,跑二分图匹配就行了。
红色是实际匹配的边,蓝色是建了没匹配的边,绿色是对应的图形。
Problem L
Upsolved by zerol. (-1)
题意:给一个网格图,相邻的平行边之间的距离为 1 或 5,求两点间的最短路,要求每个路口必须拐弯。
题解:一通观察,乱搞。如果横向和纵向之间的格子数不一样就需要绕远路,最好是在 1 的地方绕,注意 1 的地方可能在起点和终点构成的矩形外侧。
Problem M
Solved by ultmaster. 03:47 (+1)
One,Two,Three,AK
Problem A
Unsolved.
Problem B
Solved by Xiejiadong. 01:13:59(+)
Problem C
Solved by dreamcloud. 00:38 (+)
Problem D
Solved by dreamcloud. 02:00 (+)
题意:数列染色,强制在线,支持区间染色和询问某种颜色的数量。
题解:由于颜色数众多,所以没法线段树。用 set 维护所有不相交区间的端点和颜色,同时数组维护每种颜色的出现次数,每次询问至多增加一个区间,对于与之相交的区间,进行删除或者切分。这题还可以分块做。
Problem E
Solved by ultmaster. 01:24 (+)
Problem F
Solved by ultmaster. 00:29 (+1)
Problem G
Solved by zerol. 02:15 (+)
题解:有树形的与非门组成的电路,有些门坏了,会一直输出 0 或 1,求有多少种不同的输入能使输出结果错误。
题解:树形 dp。状态 2×2,表示预测值和实际值分别为 0 或 1 的情况。
Problem H
Solved by kblack. 00:08 (+)
温暖的签到。
Problem I
Solved by zerol. 01:13 (+)
Problem J
Solved by ultmaster. 00:44 (+)
Problem K
Solved by kblack. 04:23 (+2)
题意:一个矩阵,四种图形,问能否用制定方式铺满。
题解:图形 $1$ 相当于他和四周有一个连接,图形 $2$ 相当于他和四周有两个连接,拆分成对应数量的点,跑二分图匹配就行了。
红色是实际匹配的边,蓝色是建了没匹配的边,绿色是对应的图形。
Problem L
Upsolved by zerol. (-1)
题意:给一个网格图,相邻的平行边之间的距离为 1 或 5,求两点间的最短路,要求每个路口必须拐弯。
题解:一通观察,乱搞。如果横向和纵向之间的格子数不一样就需要绕远路,最好是在 1 的地方绕,注意 1 的地方可能在起点和终点构成的矩形外侧。
Problem M
Solved by ultmaster. 03:47 (+1)