F题我觉得第一步找到一个大于 $n/2$ 的数就行,期望是4步。记已知的最大数字是 $a$,这样每个数字在知道了模 $a$ 的余数之后只有2种可能,且如果小的那个已知那它必然是大的那个。这样还可以把 $a$ 更新的更大。而且每一次更新后 $n-a$ 的期望大小会除以2。感觉上最后的总期望步数在 $ n + 2 \log n \sim n + 3 \log n $ 之间。我本地跑 $ n = 20000 $ 的最大步数不超过 $20035$。
2021.10月 月赛题解
changtiaoraplanqiu edited 4 年,4 月前
花絮
- 先庆祝一下月赛暂时从双月赛变回月赛
- 第一次命题月赛, 所以十分害怕被大规模 ak, 就把题目都加强了一遍
- 包括把 D 题求 Bob 获胜的概率改成求 Alice 获胜的概率…没想到真能坑到人 @MAOoo
- F 题 感觉并不是很难, 验题的时候也确实是大家随手做的题, 不知道是不是赛前改小了 $n$ 的范围的缘故
- E 题原本是求值的和而不是异或… 感觉太简单了. 不过其实异或也挺无聊的…
- C 题是个比较基础的多项式EXP, 加进入增加一下数学浓度
- B 是加进去的签到
- A 题是个啥我也不知道
- 有可疑行为的选手已被打星, 如果觉得是被冤枉的可以来申诉
更新
- F 题更优秀的做法 MAOoo 在评论区贴了
- A.C.D.E.F 的 std
正文
本次 EOJ 月赛由华东师范大学 ACM 团队与华东师大二附中信息学竞赛组联合举办。首先,感谢以下同学为本次月赛命题做出的贡献:
| 命题 | changtiaoraplanqiu Xiejiadong |
|---|---|
| 造题 | changtiaoraplanqiu Xiejiadong cubercsl Eugen_von_Savoyen |
| 验题 | MorphLing naitir xryjr233 Kilo_5723 |
感谢华东师范大学肖春芸老师、华东师范大学第二附属中学金靖老师的组织策划,使得 EOJ 月赛能够圆满完成。此外,感谢 EOJ 运维团队为月赛提供了重要的技术支持。
A. Gold
首先注意到一个事实:一个障碍可以视作一个以其为对角线的正方形区域,这个区域一定是 Wave 无法经过的。
但是直接计算这些正方形的面积并是错误的,还少算了一部分无法经过的区域。
具体地,当两个正方形(蓝色和紫色)以如下左图方式相交时,左右凹陷部分(绿色)各自需要补上(也可能只有一边要补),因为 Wave 一旦经过绿色区域则必定会进入蓝色和紫色区域之一;但如下右图方式相交时,上下凹陷部分(红色)不需要补,因为红色区域是 Wave 可能经过的。
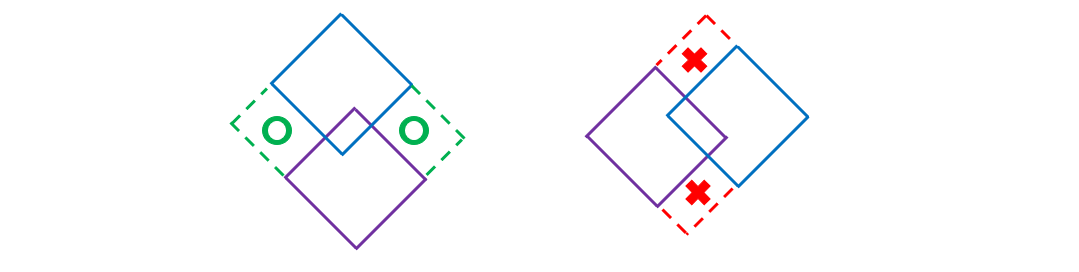
不妨先考虑一个弱一些的问题:只考虑补全左侧的凹陷部分,暂不考虑右侧。那么我们可以把一个障碍视作一个以其为斜边的等腰直角三角形(直角顶点在左侧),然后考虑用扫描线计算只考虑左半边时 Wave 无法经过的区域。
考虑如下左图,将三角形的斜边沿两条直角边投影到右边远处的一条直线上,取投影线段(红色线段)来表示这个三角形的位置,然后将所有斜边按横坐标从大到小排序,从右到左扫描。
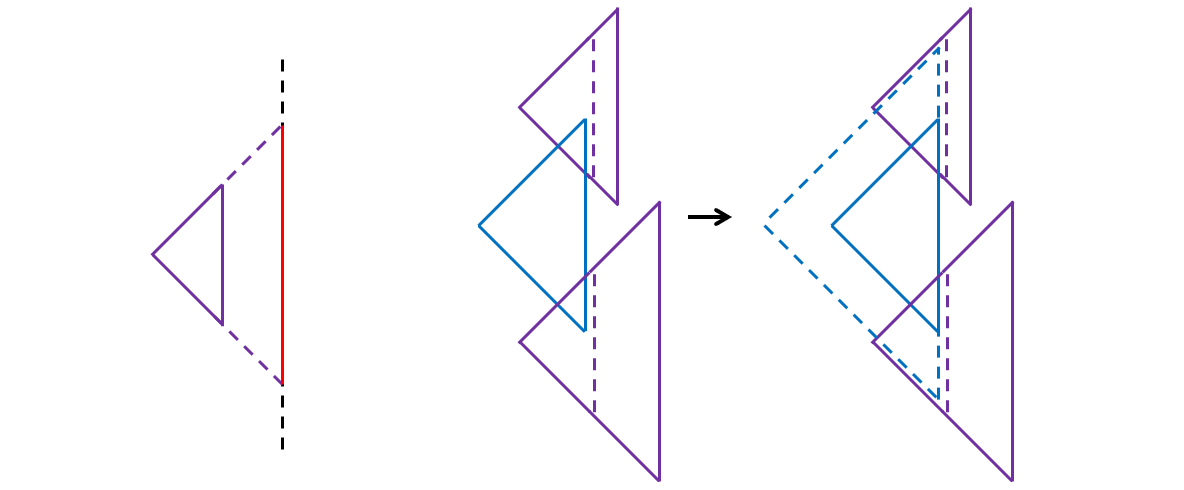
以斜边纵坐标为关键字用平衡树维护当前扫描到的横坐标上的所有三角形,如上右图,紫色虚线是当前维护的集合,考虑加入一个三角形的斜边(蓝色三角形),首先在集合中找到这条斜边上端点和下端点所在的线段(上下两条紫色虚线段),然后将这条斜边的上下端点分别扩充到这两条线段的上下端点,就形成了一个更大的(蓝色虚线所示的)三角形。
根据前面的分析,这个更大的三角形才是实际上 Wave 无法经过的被这个障碍挡掉的完整区域(相当于补全了上下两个朝左的凹陷),那么我们求这些补全过的三角形的面积并,就是答案了。
但是我们只做了左边一半,右边一半对应的三角形面积并是类似的,所以可能想到的思路是把问题转化为:
- 给定 $2m$ 个斜边竖直的等腰直角三角形(但是有左右两种朝向),求它们的面积并。
但是直接解决这个问题比较困难,我们还是继续分析题目的性质。
注意到如果一个朝左的等腰直角三角形区域是 Wave 不能经过的,那么其对应的右边对称部分也是 Wave 不能经过的,反之同理。所以我们可以把每个等腰直角三角形进一步补成一个斜着的正方形,然后问题就转化为了:
- 求 $2m$ 个斜着的正方形的面积并。
矩形面积并是经典的扫描线问题,在本题中将坐标轴转 $45^{\circ}$ 后用线段树维护即可求出答案。
一开始预处理三角形时用到的平衡树可以用 set 实现。
时间复杂度为 $O(m\log V)$,其中 $V$ 是坐标范围。
B. Secret
所有知道秘密的人作为初始节点集合,显然,我们要解决的问题就是对于每一个节点,知道他们到初始节点集合中所有点距离中的最短距离。
因为假设我们已经知道了点 $x$ 的最短距离是 $d_x$ ,消息第一天传距离 $k$, 第二天传距离 $2k$ ,那么点 $x$ 最早接受到消息的天数也就是满足 $\sum_{i=1}^y ik \ge d_x$ 的最小 $y$ ,这个简单计算就可以得到了。
于是剩下的问题就是如何知道每一个点到初始节点集合中所有点距离中的最短距离。
这个很容易用 BFS 解决,因为所有的边长度都是 $1$。将所有的初始节点集合加入队列,距离标记为 $0$,依次拓展即可得到每一个点的最短距离。
时间复杂度为 $O(n+m)$。
C. 洋葱圈
考虑长度为 $a_i$ 的倍数的洋葱圈的指数生成函数
$$
g_i(x) = (a_i - 1)!\frac{x^{a_i}}{a_i!} + (2a_i - 1)!\frac{x^{2a_i}}{2a_i!} + (3a_i - 1)!\frac{x^{3a_i}}{3a_i!} + …
\ = \frac{x^{a_i}}{a_i} + \frac{x^{2a_i}}{2a_i} + \frac{x^{3a_i}}{3a_i} + …
$$
接收长度为 $a_i$ 的倍数的盘子的生成函数即为
$$
g_i(x) + \frac{g_i(x)^2}{2!} + \frac{g_i(x)^3}{3!} + \dots = e^{g_i(x)}
$$
所有盘子的生成函数为
$$
e^{g_1(x)} \cdot e^{g_2(x)} \cdots e^{g_m(x)}
\ = e^{g_1(x) + g_2(x) + \dots + g_m(x)}
$$
把所有的 $g(x)$ 相加只需要 $nlogn$ 的时间.
再求一个多项式 EXP 即可.
时间复杂度 $O(nlog^2n)$.
D. 赌怪
值域 $1e18$, 总共抽 $10000$ 张牌, 输出精确到六位小数.
所以可以认为抽到的牌是互不相同的.
考虑 Bob 获胜的概率.
问题等价于把 Alice 和 Bob 抽到的牌排完序, Alice 最小的牌小于 Bob 最小的牌, Alice 次小的牌小于Bob 次小的牌…. 的概率.
实际上是个卡特兰数.
$$
\frac{\binom{2n}{n} \frac{1}{n + 1}}{\binom{2n}{n}} = \frac{1}{n + 1}
$$
E. 异或树
先开一个大根堆.
然后 dfs 一遍, 建出可持久化字典树, 并且每个点把自己和祖先的异或最大值扔进堆里.
循环 $k$ 次, 每次从堆中弹出最大值, 假设被弹出的点已经被弹出来了 $x$ 次, 则在字典树上搜它的第 $x + 1$ 大的异或值, 再扔进堆里即可.
时间复杂度 $O(30n + k(logn + 30))$
F. oh my cuber
-
第一版 $\frac{3n}{2} + 100$
-
第二版询问次数改到 $\frac{6n}{5}$, $n \ge 2e5$.
-
最后发现 $n$ 开到 $10000$ 都行.
思路是先问出一个尽可能大的值, 然后用这个值去询问其他的.
比如先问出一个大于 $\frac{5n}{6}$ 的值, 再用 $n - 1$ 次询问求出其他数模它的值.只有 $\frac{n}{6}$ 个值会出现两次. 再用 $\frac{n}{6}$ 次询问即可区分出两个数.
最后询问次数就是问出这个比较大的值的次数加上后面的询问的次数.
具体要问多大自己打个表找最优解肯定没问题. 不过估计一下问1000次也是可以的.
询问次数随着 $n$ 的增大是越来越接近 $n$ 的.
int base = 1000;
int n = 13000;
for (int i = 1; i <= base / 2; i++) {
int cnt1 = ((double)i / base) * n;
long double p = 1;
int cnt2 = 0;
while (p > 0.0005) {
cnt2++;
p *= (1 - (1.0 * i / base) * (1.0 * i / base) * 0.5);
}
double x = 1.0 * (cnt1 + cnt2) / n;
dbg(i, cnt1, cnt2, x);
}
扫描二维码关注我们的微信公众号,获得更多信息。本次月赛的获奖名单和后续竞赛通知将通过公众号发布。

您是对的 qwq