2024 上海市大学生编程新锐挑战赛题解

sha7dow edited 4 周，1 天前

Problem A. Rush for a place

令睡觉的时间点为 $x$，睡醒的时间点为 $y$，分情况讨论：

当 $x = p$ 时，因为至少睡 $1$ 个单位时间，所以一定会睡过 $p$，不合法。
当 $x > p$ 时，是否睡觉并不会影响答案，所以当 $p \equiv 0 \pmod{t}$ 时，无论睡多久都合法，否则都不合法。
当 $x < p$ 时，只有当 $y \leqslant p$ 且 $(p - y) \equiv 0 \pmod{t}$ 时才合法，否则不合法。

第一部分直接忽略，第二部分显然可以 $O(1)$ 计算方案数。
对于第三部分，可以先考虑枚举 $x$。对于固定的 $x$，合法的方案数可以 $O(1)$ 求出，为 $\lceil \frac{p - x}{t} \rceil$。
但是如果直接枚举 $x$ 这部分的时间复杂度为 $O(p)$，无法通过，考虑如何优化。
不难发现第三部分的式子是一个等差数列，因此利用等差数列求和公式可以 $O(1)$ 求出。

单个测试用例的时间复杂度：$O(1)$。

Problem B. nindeECNUOJgule

根据题意，我们需要找出两字符串之间每一个字符的数量差异，对于每一种字符，最终两串中剩余的应为该字符数量更少的串中这一字符的数量。所以我们可以有两种做法：

将两字符串内部从小到大排序使用双指针扫描，如果字符相同则跳过（即保留）这两个字符，否则删去两个字符中较小的那一个并将删去字符的串的指针右移 $1$ ，继续比较直到结束。在末尾未被比较的字符也应被删除。
在两字符串中对每一个字符计数。最终保留下来的每一种字符数量是两串中该字符数量的更小的值，然后使用每一个字符串一开始的每一种字符数量减去保留下来的字符数量就是应删去的字符数量。

时间复杂度：$O(len)$

Problem C. sha7dow loves rand function

设生成的随机数列最小正周期为 $t$，则 $\forall i \leqslant n,\ t \mid t_i$，从而 $t \mid \gcd\limits_{i \leqslant n} t_i$，
同时 $\forall i \leqslant m,\ t \nmid s_i$，只需判断所有 $s_i$ 都不是 $t$ 的倍数，显然取 $t=\gcd\limits_{i \leqslant n} t_i$ 最优，若可行则取 $a=b=1,\ c=\gcd\limits_{i \leqslant n} t_i$ 即可。

Problem D. 2D Pinball (Easy)

这是一道模拟题。根据题意，我们可以按照题中信息求出每一个状态（行、列位置以及方向）对应的下一状态。我们可以发现，弹球在最终一定会进入一个状态循环，所以我们在弹球没有进入循环时继续模拟同时记录当前状态对应的步数，只要进入循环则可以通过之前在这个状态的步数以及路径直接求出目标状态。

时间复杂度：$O(nm)$

由于时限是按照困难版本给的且数据只有 $10^9$ ，所以放过了一些常数较小的纯模拟提交。

Problem E. 2D Pinball (Hard)

根据简单版本，我们已经求出了每一个状态过一秒后的下一个状态，我们可以使用倍增的方法求出每一个状态过两秒、四秒、…、 $2^k$ 秒的状态。首先预处理出每一个状态的上述跳转的状态，接下来对于每一个位置我们可以根据其等待时间的二进制在状态之间跳转，处理一次询问只需要 $\log(t_i)$ 次跳转。

时间复杂度：$O(nm\log(\max(t_i)) + T\log(\max(t_i)))$

Problem F. sha7dow loves data structure

不考虑连边限制，则取 $m=1$，$H$ 中所有点都向 $T$ 中节点 $1$ 连边即可。
分治给 $H$ 的子树连边，每个子树额外连边最多只有两个叶子节点，假设当前递归的子树根节点为 $x$，则为这两个叶子节点选择与 $x$ 的父节点连边的 $T$ 中节点连边，子树中其余节点先连向 $T$ 中同一新节点，然后递归所有不包含这两个叶子节点的极大子树，显然 $T$ 为树形结构。
观察发现这样递归每个子树会留下每层编号最小和最大的节点（包括次小和次大的叶子节点，因为最小和最大的叶子节点已经选择与 $x$ 的父节点连边的 $T$ 中节点连边）形成的一条链连向 $T$ 中同一节点，除去次小和次大的叶子节点，将剩下的这条链两侧分别按对称的形式选择 $T$ 中节点连边，则 $T$ 中每个节点连边最多不会超过 $4\times(1+2)+3=15$ 次。

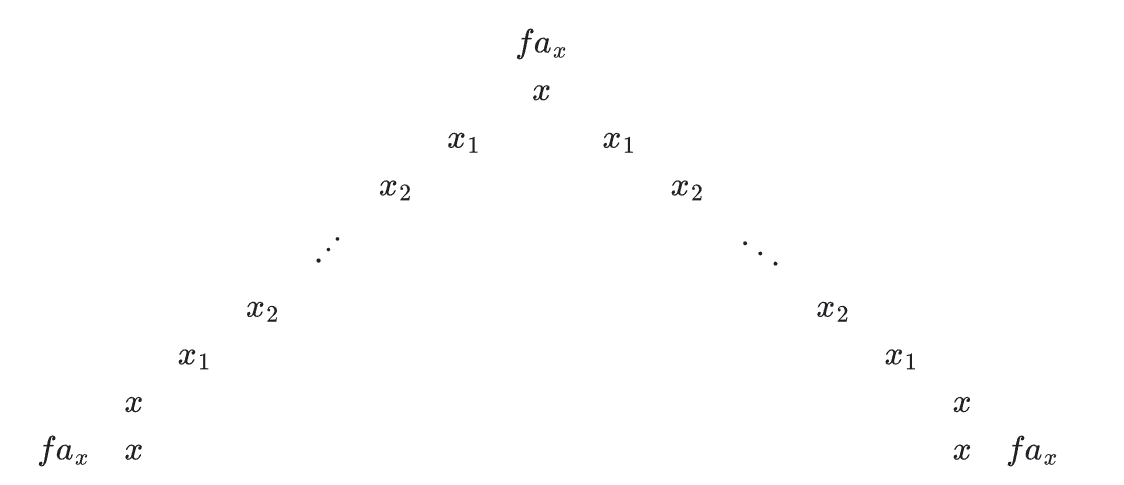
对于原满二叉树的一个以 $x$ 为根的子树，图中每个 $H$ 中节点处的值为对应的选择连边的 $T$ 中节点，当前递归时 $fa_x$ 已知，$x$，$x_1$，$x_2$ 等均为 $T$ 中新建的节点，空白部分在进一步递归时确定。

Problem G. Roll the dice

打表找规律题。

记 $dx = |sx - tx|, \ dy = |sy - ty|$。
用 BFS 将表打出来，不难发现当 $dx \geqslant 2$ 且 $dy \geqslant 2$ 时，最少操作次数就是 $dx + dy$。否则以 $dx \leqslant 1$ 为例：
当 $dy \equiv 0 \pmod{4}$ 时，除了 $dy = 0$ 且 $dx = 1$ 的情况，最少操作次数仍为 $dx + dy$；否则除了 $dx = 1$ 且 $dy = 1$ 的情况需要特判，其它情况的答案均为 $dx + dy + 2$。$dy \leqslant 1$ 的情况同理。此外，还需要特判 $n \leqslant 2$ 或 $m \leqslant 2$ 的情况，不再赘述。
单个测试用例的时间复杂度：$O(1)$。

上面的结论均可以严谨证明，略。

Problem H. 164ovo dislikes triangles

容易得知， $n = 2,3,5$ 时是没有可行的方案的。 $n = 6,7,8$ 的构造方案如下（请注意：题面中说明了小三角形的大小可以不相等），同时如果 $n = k$ 时成立， $n = k + 3$ 时也一定成立。

所以只有 $n=2,3,5$ 时输出 No ，否则输出 Yes 。

Problem I. sha7dow loves sqrt technology

若只求区间逆序对数，而题目给出的区间递归生成，则对每个区间分别求逆序对数时间复杂度为 $O(n\log^2n)$。考虑多路归并同时求出所有区间逆序对数，归并时需要维护前缀区间大于当前数的数的个数，可用树状数组实现，单次归并时间复杂度 $O(n\log n)$，总时间复杂度也为 $O(n\log^2n)$。奇偶子区间合并而成的序列逆序对数可由三部分组成，奇子区间的逆序对数和乘偶子区间的个数，偶子区间的逆序对数和乘奇子区间的个数，跨奇偶子区间的逆序对数。前两部分可由子区间逆序对数快速求出，最后一部分将归并合并的树状数组分奇偶存放，类似正常逆序对数求出即可。

Problem J. Count S

定位为最简单的三道题之一，但是开始的时候榜歪了。。。

因为 $n \leqslant 50$，所以只需要暴力即可。具体地，$O(n^2)$ 枚举 $S$ 图最右上角的点，然后 $O(n)$ 枚举 $S$ 图大小，最后 $O(n)$ 检查是否所有点均为黑色。总的时间复杂度：$O(n^4)$。

可以用二维前缀和优化到 $O(n^3)$，但作为签到题所以没有加强。

7 0

2024 上海市大学生编程新锐挑战赛题解