A题“发现后手必胜的 n 的二进制表达里只有偶数位可能为 1。”,这个可以加上证明吗,菜鸡列出后手必胜了也没有发现
2019.9 月赛题解
Xiejiadong edited 4 年,7 月前
花絮
- 这次的题目,码量很少。
- 久违的温暖场了吧。全面开花。
- 不过没有人 AK ,还是有点诧异。
- 事实上,Cuber QQ 并没有参加军训,所以他每天都在划水。
- 事实上,Cuber QQ 的唱跳大家并没有领略过。
- 事实上,丽娃河没有鸭子,荷花倒是不少。
- 好像我接锅月赛以后,
Monthly变成了Every Two Months,说不定以后变成Quarterly了也说不定。

| # | Tag | Idea | Developer | Tester |
|---|---|---|---|---|
| A | 博弈 | cs2017 | Xiejiadong | Kilo_5723 10175101214 |
| B | 贪心 | Xiejiadong | Xiejiadong | 10175101214 oxx1108 Grunt |
| C | 签到 | Weaver_zhu | Weaver_zhu | 10175101214 oxx1108 |
| D | 数学 | Kilo_5723 | Kilo_5723 | 10175101214 Grunt |
| E | DP | Grunt | Grunt | 10175101214 Xiejiadong |
Problem A
First Solved:ustczml
本题的模型是一个平等博弈的游戏。
题目中的 DAG 可以通过 SG 函数 $O(n)$ 求出先手必胜还是后手必胜。
把所有后手必胜的局面列举出来,发现后手必胜的 $n$ 的二进制表达里只有偶数位可能为 $1$。
可以证明,所有符合这种性质的 $n$ 都能找到后手必胜的策略,而不符合这种性质的 $n$ 都有先手必胜的策略。因此,每个 $n$ 的奇数二进制位是否都为 $0$ 就是答案。
Comments
10175101214 : 这题博弈和我以往做的不太一样,挺有意思的。
Problem B
First Solved:suzukaze
因为题目保证了不包含数字 $0$ ,很显然的,要求最小的最大,我们一定会尽可能的把数位先分均匀。
较小的位数一定是 $\lfloor \frac{n}{k}
\rfloor $ ,我们可以直接算出位数为 $\lfloor \frac{n}{k}\rfloor $ 的个数和位数为 $(\lfloor \frac{n}{k}\rfloor +1)$ 的个数。
最小的数一定产生在位数为 $\lfloor \frac{n}{k}
\rfloor $ 的数中,于是我们会贪心地把大的数字分给他们。
分配的方案一定是,按照数字从大到小,依次分给当前可能最小的数。
当前可能最小的数的数量是会发生变化的,因为一旦当前所在位所分配的数字不同,就一定会产生大小的差异,也就是说,当前可能最小的数一定会越来越小。
还可以发现的是,最小的数,一定是一个数字从大到小的非降数字构成的,也就是相同的数字只可能在同一段出现(这个从上面贪心的策略可以得到)。
于是对于最小值,我们模拟贪心的过程,每一个数字一次性放入,对于取模的结果,可以预处理得到。
Comments
Xiejiadong : 我和验题人都没有考虑到大力预处理暴力就能过的问题。所以变成了纯·签到题。如果加上在线修改,就能卡掉他们了吧。
Problem C
First Solved:ReTleWa
因为受到的伤害是固定的,所以问题不在于哪个时机 Cuber QQ 打出最后一击,而是是否能在每次外界攻击前配合之前的攻击打死小兵,我们只需要在这次攻击结算前一秒打出最后一击就行了。
而要求第一下最晚,就恰好是从 $ans$ 到 $a_i-1$ (也就是这次攻击结算前一秒) 恰好一直连续攻击 $x$ 次配合外界攻击击杀小兵,显然这样是可行的又是最好的方案。注意需要过滤掉超过 $10^8$ 的攻击,或者干脆加一个时间为 $10^8+1$,伤害为 $n$ 的攻击。
然后就是从小到大枚举每次攻击前一秒,看看是否可以给出最后一击,然后更新答案。注意时间可能相等,需要一次处理完所有 $a_i$ 相同的攻击,也要注意随之而来的爆 int 问题。
Comments
oxx1108 : 感觉这题的坑,挖的有些许生硬。
Xiejiadong : 这题的题面进行了无数次的修正,希望最终版本没问题吧。
Problem D
First Solved:SuperSodaSea
我们只关心鸭子是否分布在一个半圆中,所以鸭子离圆心的距离不重要。我们可以假设鸭子都落在圆周上。
如果所有的鸭子分布在同一个半圆中,那么让鸭子面朝圆心,所有的鸭子一定都在某一只鸭子的右手边。
令所有鸭子都在第 $i$ 只鸭子的右手边是事件 $P_i$,则 $P_i$ 发生的概率是 $2^{1-n}$。那么,$n$ 只鸭子分布在其中任何一只鸭子的右手边的概率是不是 $n \cdot 2^{1-n}$ ?
答案是肯定的。可以证明 $P_i$ 和 $P_j$ ($i \neq j$) 不会同时发生(因为 $n$ 只鸭子不会同时分布在 $i$ 和 $j$ 的右手边,如果 $i$ 在 $j$ 的右手边,$j$ 就一定在 $i$ 的左手边)。对于 $n$ 个不会同时发生的事件,它们之中任何一个发生的的概率就是每一个发生的概率之和,也就是说,$n$ 只鸭子分布在其中任何一只鸭子的右手边的概率是 $n \cdot 2^{1-n}$。
因此,$n$ 只鸭子分布在同一个半圆中的概率就是 $n \cdot 2^{1-n}$。
更多解法,可以查阅知乎。
Comments
Grunt : 这题知乎上有答案。
Kilo_5723 : 当时是看到了 $4$ 只鸭子的题目,发现可以推广,就拿过来了。
Xiejiadong : 能自己完整做出来的人,估计不是很多吧。
Problem E
First Solved:Fuck_you_asshole
解法 1 :
by 10175101214
Part One
考虑在每次插入一个数后维护若干桶( Bucket )。
每个桶记录一下信息:
当前值 $ curval$ :表示这个桶已经确定的前 $i$ 位二进制位,桶里面的所有元素前 $i$ 位二进制位的与的结果 $x$ 需要满足 $ (x^{’})\&(curval^{’})==(curval^{’}) $($ x^{’} $ 为 $ x $ 的前 $ i $ 位二进制位, $ curval^{’} $ 为 $ curval $ 的前 $ i $ 位二进制位)。
剩下需要考虑的位置 $ j $ :由于前 $ i $ 位已经确定,所以剩下还需要考虑( $ 32-i $ )位。
- 元素 $ num $ :表示桶里面放的元素(最多 $ 3 $ 个,若一个桶中有 $ 3 $ 个元素时,则表示可以用 $ curval $ 更新答案了,此时需要将桶分裂)。
- 指针 $ point $ :记录桶分裂后,新的桶的地址。
- 标识 $ flag $ :标记桶是否分裂过。
每个桶支持操作:
- 插入 $ insert $ :插入一个元素,若插入导致桶溢出(达到 $ 3 $ 个数),则桶分裂。
- 分裂 $ split $ :一个桶分裂成 $j$ 个桶,分裂后需要重新分配桶中的三个元素。
计算最大的可能值 $ maxval $ :由于前 $ i $ 位已经确定,最大可能值为剩下 $ j $ 位全为 $ 1 $ ,即 $ curval+( 1< < j)-1 $ 。
Part Two 案例分析
考虑插入 $ 9 10 11 15 $
1、插入 $ 9 $ 和 $ 10 $ :直接插入
curval:0
j:31
flag=false
num:9
10
2、插入 $ 11 $ :由于桶中元素已经满了,所以需要将桶分裂成 $ 31 $ 个桶:其 $ curval $ 分别为: $ 1,2,4,8,… $ ; $ j $ 分别为 $ 0,1,2,3,… $ 。表示含义枚举下一个 $ 1 $ 填在哪里,若下一个 $ 1 $ 填为第 $ 0 $ 位,则答案变成 $ 1 $ ,此时所有位都确定(因为下一位填在第 $ 0 $ 位意味着第 $ 1-31 $ 位都不可能填),后面的桶类似。现在考虑将 $ 9 10 11 $ 重新分配成 $ 31 $ 个新的桶中:由于 $ 9 $ 的二进制是 $ 1001 $ ,所以对 $ curval $ 为 $ 1 $ 和 $ 8 $ 的桶有贡献,所以插入在这两个桶中,类似 $ 10 $ 放入 $ curval $ 为 $ 2 $ 和 $ 8 $ 的桶, $ 11 $ 放入 $ curval $ 为 $ 1,2,8 $ 的桶中(注意:若插入过程新桶也满了,如例子中 $ curval $ 为 $ 8 $ 的桶,则递归这个过程)。(此时 $ ans=8 $ )
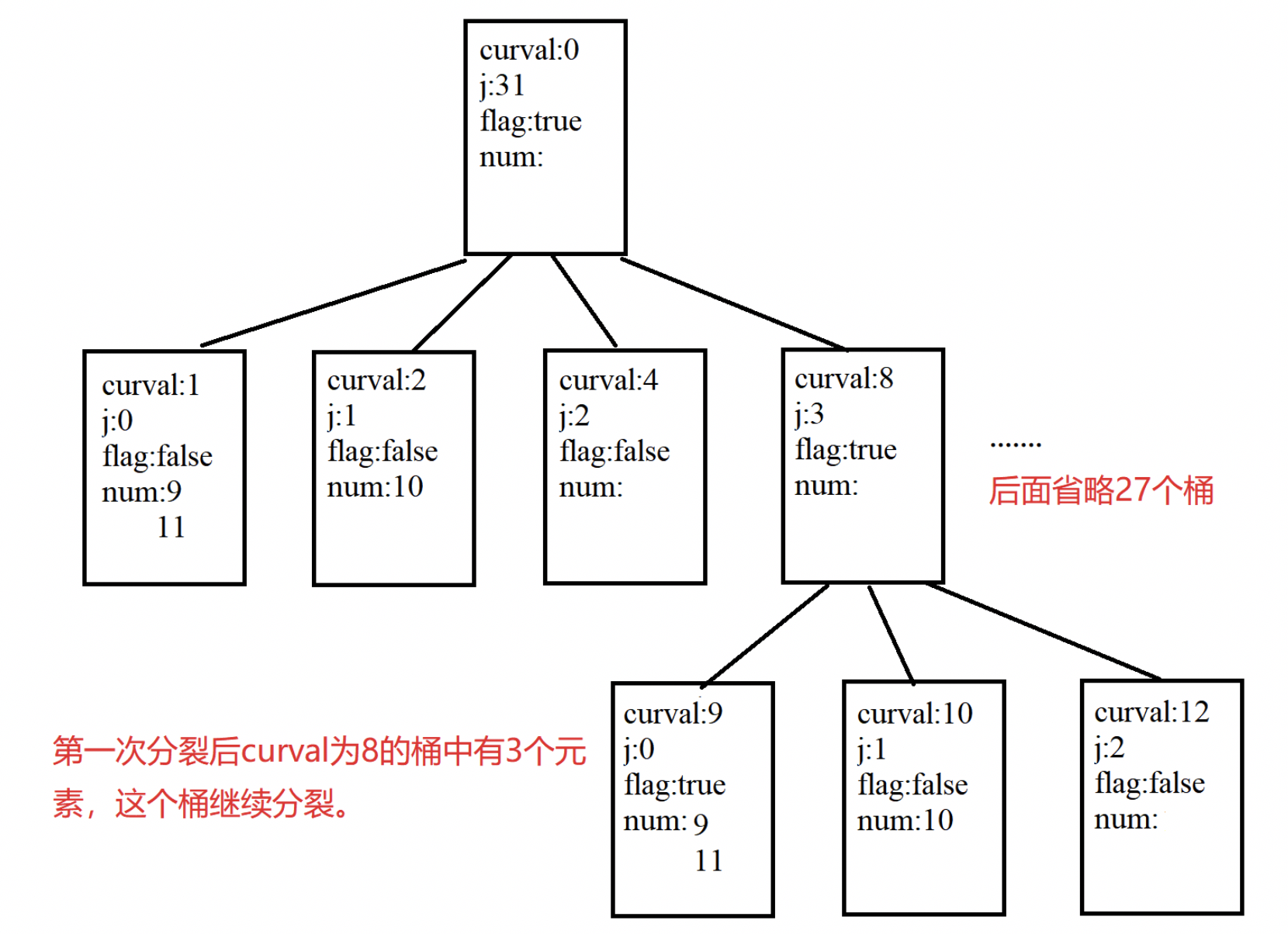
3、插入 $ 15 $ (此时 $ ans=9 $ )
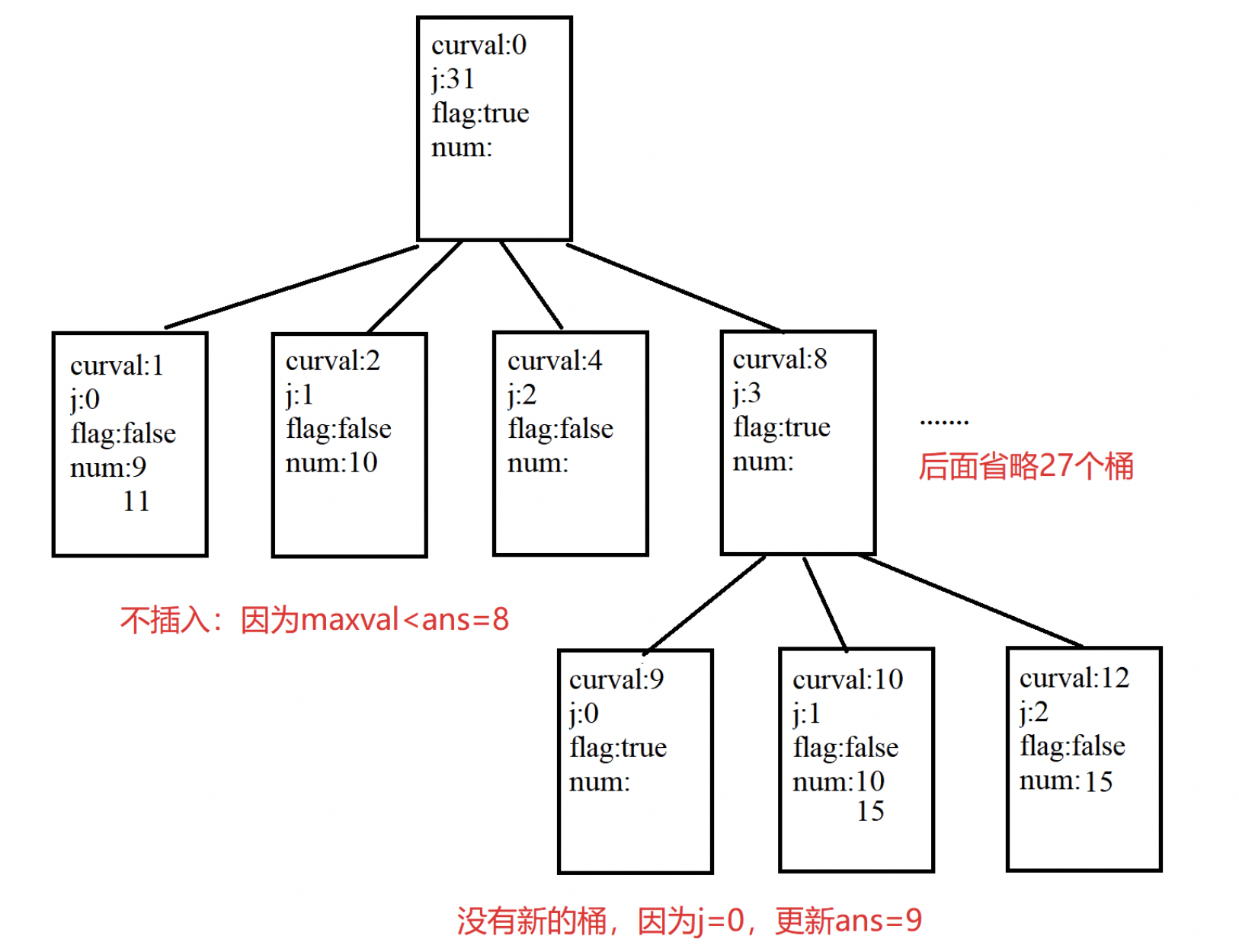
Part Three 复杂度证明
1、插入过程:如果插入一个数桶没有满则直接插入,若需要桶分裂,假设分离了 $ j=k $ 的桶,则所以 $ j < k $ 的桶都无需继续考虑,因为 $ maxval < ans $ ,而每一次的分裂需要确定的二进制位数至少减少 $ 1 $ ,将原来桶中的 $ 3 $ 个数重新分配需要 $ O(log(n)) $ 的复杂度,而重新分配过程中最多继续分裂一个桶,所以插入一个数最多分裂 $ log(n) $ 个桶,所以插入复杂度为 $ O(log(n)^2) $ 。
2、查询过程:动态维护 $ ans $ ,查询 $ O(1) $ 。
解法二
与解法一大同小异,但是时间复杂度相差一个 $log$ 。
首先考虑离线的版本:
可以用广为人知的 SOS DP解决。
具体做法是将去重后的插入按操作顺序存为数组 $a_n$。用类似SOS DP的做法, $F[mask]$ 存的是一个大小为 $3$ 的小顶堆, 表示满足 $a_i\&mask=mask$ 的最小的 $3$ 个 $i$ 。
对于每个询问,从高到低逐位确定答案的那一位是否可以为 $1$ , 当前 $mask$ 当且仅当 $F[mask]$ 的最大值小于本查询的时间 tag 时可以取到。
再考虑一个暴力的做法:
维护一个数组 $cnt[M]$ , 对于每个不重复的插入 $a_i$ , 枚举所有满足 $mask\&a_i=mask$ 的 $mask$ , 令 $cnt[mask]\mathrel{+}=1$ 。查询同样是从高到低逐位确定答案, 当前 $mask$ 当且仅当 $cnt[mask]\ge 3$ 时可以取到,这样可以做到动态插入和查询,但显然复杂度过高。
考虑如何优化暴力的复杂度:
观察到冗余的操作主要在于 $cnt[i]\ge 3$ 时, $cnt$ 再增加是没有意义的。于是可以在枚举子集的过程中直接 break 掉。
最后的问题是按什么样的顺序枚举子集,这个可以参照SOS DP的方法。

具体可以参考上图中的枚举顺序。
最后我们得到了一个化离线为在线的神奇做法, 时间复杂度为 $O(n\log_2 m)$ 。
这个打表以后,很容易发现的规律吧。
好吧,我也是最后几分钟打的表,也没看多久,早知道多找找规律了QAQ