2019级新生编程能力测试
单点时限: 3.5 sec
内存限制: 256 MB
求超越函数 $f(x)=k*x^p-m^x$ ,其中 $k,m,p\in Z^+, p\ge 2,m\ge 2$ ,在闭区间中 $[a,b]$ 的最大值。
当然,由于超越函数不具有良好的函数特性,比如:超越函数不一定是单调函数。
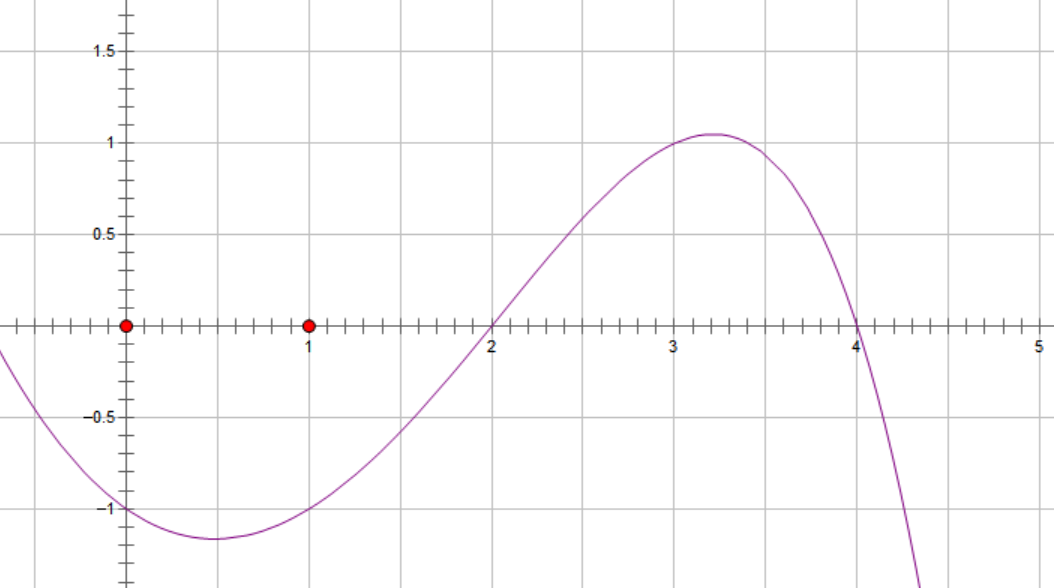
于是,为了简化问题,数据中保证 $f(x)$ 在闭区间 $[a,b]$ 中是一个单峰函数,也就是说函数 $f(x)$ 在区间 $[a, b]$ 上只有唯一的最大值点 $C$ ,而在最大值点 $C$ 的左侧,函数单调增加;在点 $C$ 的右侧,函数单调减少。
是不是感觉很简单呢?
输入格式
第一行一个整数 $t$ ,表示测试组数。
接下来 $t$ 行,每行五个整数 $k,m,p,a,b$ 。
输出格式
共 $t$ 行,每行一个小数 $x_0$ 满足 $a<x_0<b$ ,且满足 $f(x_0)$ 是 $f(x)$ 在闭区间 $[a,b]$ 上的最大值。
你的答案和标准答案的绝对误差或相对误差在 $10^{-6}$ 之内会被认为是正确的。
样例
1 1 2 2 2 4
3.21243252
提示
温馨提示
1、long double 最大范围约在$10^{4932}$,long double 输出请用prinf(“%.8Lf\n”,ans);或者强制类型转换成double都输出。(for c & c++)。
2、double 最大范围约在$10^{308}$,double 输出请用prinf(“%.8lf\n”,ans);(for c & c++)。
3、java 请使用 java.math.BigDecimal ,
4、读入数据量大,请使用 scanf(for c & c++) 。
5、请一定要认真阅读数据约定!!!!!
数据约定
$30\%$ 数据满足 $t=1,1\leq k\leq 10,2\leq m\leq 10,2\leq p\leq 10,0\leq a<b\leq 10$ ;
$50\%$ 数据满足 $1\leq t \leq 10,1\leq k\leq 100,2\leq m\leq 10,2\leq p\leq 100,0\leq a<b\leq 10^3$ ;
$70\%$ 数据满足 $1\leq t \leq 10^3,1\leq k\leq 100,2\leq m\leq 10,2\leq p\leq 100,0\leq a<b\leq 10^3$ ;
$100\%$ 数据满足 $1\leq t \leq 10^4,1\leq k\leq 10^6,2\leq m\leq 10^3,2\leq p\leq 10^6,0\leq a<b\leq 10^7$ 。