1039. 树的双亲存储法 - 数据结构与算法专题题库

单点时限: 2.0 sec

内存限制: 256 MB

前面介绍了树的链式存储结构，那么如何用顺序存储来存储一棵树呢？在顺序存储时，我们除了存储每个结点值外，还要存储树中结点与结点之间的逻辑关系（即双亲与孩子结点之间的关系）。下面介绍树的双亲存储法。

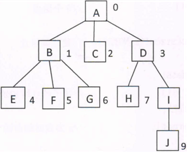
编号，从根结点（它的编号为 0）开始，按从上到下的层次顺序，每一层按从左到右的顺序，递增地依次给每一个结点一个编号，图1上标出了各个结点的编号。
存储，如果用一维数组 tree[n] 来存储图1中的这棵树，则树中每个结点存储在 tree[n] 中的下标等于它的编号值，而且在数组 tree[n] 中，每个元素是一个结构体，它包含两个成员，data 和 parent：其中 tree[i].data 存储一个结点的值， tree[i].parent 存储该结点的双亲结点在该数组中的下标。根结点 tree[O].parent=-1, 图2为图1中树的存储数组。

现在给出一棵树的顺序存储结构，打印树的后序遍历。

输入格式

第一行一个整数 $n$ $(1 \leq n \leq 100~000)$，表示有 $n$ 个节点，节点的编号从 $0$ 到 $n-1$。

接下来一行 $n$ 个整数，依次表示每个节点的双亲 (tree[i].parent)。数据保证合法，能构成一棵树，并且 tree[0].parent=-1。

输出格式

输出树的后序遍历。

样例

Input

10
-1 0 0 0 1 1 1 3 3 8

Output

4 5 6 1 2 7 9 8 3 0

1001. 栈的实现 1002. 铁路调度 1003. 数据生成器 1004. 队列的实现 1005. 座位分配 1006. 车厢调度 1007. Max Element 1008. 最小的n个和 1009. 数据整理 1010. 约瑟夫环问题 1011. 链表去重 1012. n皇后问题 1013. 迷宫搜索 1014. 构造字典序最小字符串 1015. 任务调度 1016. 快速排序 1017. 逆序对 1018. 最大最小问题 1019. 层次遍历 1020. 医疗队列 1021. 数独问题 1022. 终极背包问题 1023. 终极混合背包问题 1024. 分割回文串 1025. 树的直径 1026. 路径差 1027. 旅行商问题 1028. 数的变换 1029. 单峰序列 1030. 高级并查集 1031. 传送门（一） 1032. 传送门（三） 1033. 一元多项式乘法 1034. 表达式 1035. 恢复古诗 1036. 代码查重 1037. Take a party 1038. 小强的烦恼 1039. 树的双亲存储法 1040. A Knight's Journey 1041. 华师大卫星照片 1042. Can you do DFS? 1043. 斐波那契数列和 1044. 说出来可能不信这是排序题 1045. 最大的子串 1046. 最小等待时间 1047. 判断两个数是否相等 1048. 电话送报 1049. 简单排序题 1050. Ants 1051. 付款问题 1052. 数塔 1053. 最长连续公共子序列 1054. 整数的拆分 1055. 完全加括号的矩阵连乘积 1056. 装箱问题 1057. 统计字符串个数 1058. 子集和问题 1059. 区间覆盖 1060. 0-1背包问题 1061. 放书 1062. 经典的猜数游戏 1063. 最近点对 1064. 双人旋转赛车 1065. Hanoi Tower II 1066. Hanoi Tower III 1067. Hanoi Tower IV 1068. 奇异收缩的剪影

数据结构与算法专题题库

输入格式

输出格式

样例

题目列表

服务

开源

关于我们