EOJ Monthly 2020.9 Sponsored by TuSimple
单点时限: 1.0 sec
内存限制: 256 MB
QQ 小方是 BanG Dream 的资深玩家。每天,他都会光顾 CiRCLE 旗舰店,以在第一时间入手心仪的唱片和周边。
麻里奈小姐是 CiRCLE 旗舰店的老板。每一位在 CiRCLE 消费的顾客,都有机会从麻里奈小姐的礼物箱中抽取精美的礼品。麻里奈在礼物箱中准备了 $n$ 种不同的礼物,第 $i$ 种礼物共有 $a_i$ 件。每次抽取可以随机获得礼物箱中的一件礼物,且一件礼物一旦被顾客抽取,就不会再放回。QQ 小方是一位不折不扣的收集控,他想问问你,期望抽取多少次可以收集到每一种礼物?
为了方便讨论,我们认为,对于每一次抽取,获得礼物箱中剩余的每一件礼物的概率是等同的。例如,在如图所示的礼物箱中,下一抽抽到”五千金币”的概率是 $0.2$。
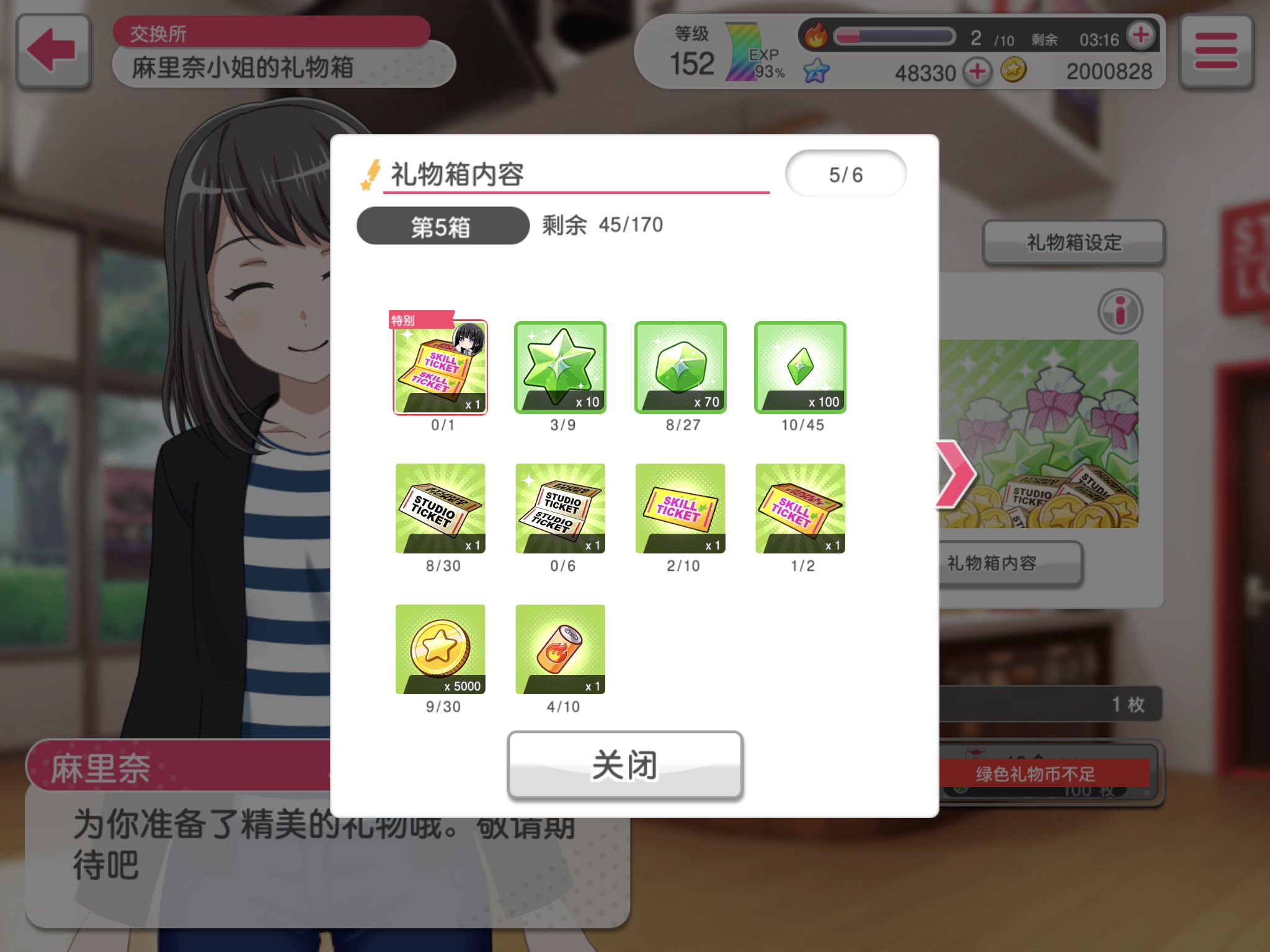
可以证明,期望的抽取次数是一个有理数。设答案为 $\frac{p}{q}$($p,q$ 为正整数),则你需要输出 $p\cdot q^{-1} \mod 998244353$,其中 $q^{-1}$ 表示正整数 $q$ 在模 $998244353$ 意义下的乘法逆元。
输入格式
第一行,一个整数 $n$($1 \le n \le 20$),表示礼物的种类数。
第二行,输入 $n$ 个空格分隔的正整数 $a_1,a_2,\dots,a_{n}$($1\le a_i \le 2000$,$n\le \sum_{i=1}^{n}a_{i} \le 2000$),分别表示每一种礼物的数量。
输出格式
设期望的抽取次数为 $\frac{p}{q}$($p,q$ 为正整数),则你需要输出 $p\cdot q^{-1} \mod 998244353$,其中 $q^{-1}$ 表示正整数 $q$ 在模 $998244353$ 意义下的乘法逆元。
样例
2 1 1
2
10 1 9 27 45 30 6 10 2 30 10
35966514
提示
对于样例一,可以发现,当且仅当抽取两次之后可以获得全部两种礼物,所以答案为 $2$。
题面所述的”五千金币”是指图中第三行第一列的礼物,现共有 $9$ 个,因为礼物箱中剩余礼物总数为 $45$,所以下一抽获得”五千金币”的概率是 $\frac{9}{45}=0.2$