2022 年上海市大学生程序设计竞赛 - 十二月赛
单点时限: 2.0 sec
内存限制: 512 MB
Foxity have a complete $n$-ary tree with a depth of $m$, $n$ is odd(Which means a tree with the depth of $m$, the leaf nodes are all in the $m$ layer, and each of the other nodes has $n$ child nodes).
This tree satisfies that the value of non-leaf node on the tree always equals to the mode(众数) of the value of its child nodes, and the value of leaf node initially equals to the remainder of its position divided by $2$(all mentioned position is from left to right, subscript starts from $1$).
As a example of intial tree when $n=3$ and $m=3$
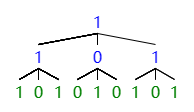
Then he have $q$ queries, each time he will modify all the leaf node of the subtree whose root node is the $l$-th node of the $k$-th level in the original tree according to the value of $f$:
$f=0$: setting $0$, meaning all it leaf nodes become $0$
$f=1$: setting $1$, meaning all it leaf nodes become $1$
$f=2$: setting flip, meaning $1$ become $0$, and $0$ become $1$
Then update the non-leaf nodes of the tree to satisfy their properties.
After each query, Foxitu wants to know how many nodes satisfying its value equals to $1$.
输入格式
First line contains $3$ integers $n,m,q(1 \le n,m,n^m \le 10^9 ,n \mod 2=1, 1 \le q \le 2 \times 10^3)$, which means the number of child nodes of non-leaf nodes, the depth of the tree, the number of queries.
Following with $q$ lines,each line contains $3$ integer $k,l,f(1 \le k \le m,1 \le l \le n^{k-1},0 \le f \le 2)$, which means the depth of the root of the subtree, the postion of the root of the subtree, the number of modify operator he choose.
输出格式
$q$ lines, which means the number of nodes satisfying its value is $1$ after the current update.
样例
3 3 10 3 9 1 2 1 1 1 1 1 2 2 1 3 7 0 3 8 1 2 3 2 1 1 2 1 1 2 3 5 0
8 9 13 13 12 12 10 3 10 9