2023 年上海市大学生程序设计竞赛 - 八月赛

现在是彩蛋时间！

有 $n$ 个彩蛋分布于 $k\times k$ 的网格图的端点上，每个彩蛋的坐标为 $(x_i,y_i)$ ，其中 $(1,1),(k,k)$ 两个端点上一定有一个彩蛋。

选取网格图中的 $m$ 条边将这些彩蛋相连（每条边都连接网格图中距离为 1 的两个点）。当你在网格图中行走时，你只能走向右或向上的边，即若当前你在 $(x,y)$ 点，你只能走另一个端点为 $(x+1,y)$ 或 $(x,y+1)$ 的边。从任意一个点出发一定可以到达 $(k,k)$ 点。

你会进行 $Q$ 次彩蛋游戏，每次游戏你会出现在其中一个彩蛋所在端点上，随后你可以从当前点出发，走向右或向上的边获取彩蛋，每当你到达一个点时，若这个点上彩蛋的种类与你之前获取的都不同，你可以获取它。

你随时可以回到本次游戏的出发点，走另一条路径。

数据保证从 $(1,1)$ 出发进行一次彩蛋游戏一定可以到达所有点。

每次游戏开始时，之前的游戏状态都会重置，即之前所有获得的彩蛋都会被放置回原处，你身上也不再持有彩蛋。现在请你求出，每次游戏你最多可以获取多少彩蛋。

下图为样例的彩蛋分布情况。

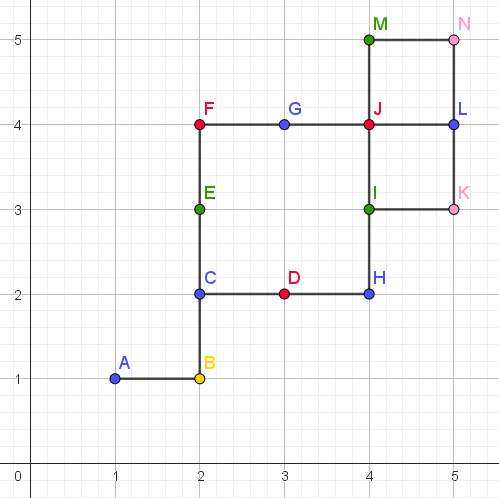
在这个网格图中，共有五种类型的彩蛋（分别用五种颜色表示），从 $D$ 点出发分别可以获取红色（$D,J$)，蓝色（$H,L$)，绿色（$I,M$)，粉色（$K,N$)四种类型的彩蛋，因此从 $D$ 点开始进行的彩蛋游戏答案为 4。