2024 上海市大学生编程新锐挑战赛
D. 2D Pinball (Easy)
单点时限: 4.0 sec
内存限制: 1024 MB
请注意：本题存在对应的困难版本，两版本仅数据范围不同。保证通过了困难版本的提交可以通过简单版本。在当前版本中， $T = 1$ 。
$\texttt{SpadeZ}$ 有一个长方形的弹球桌，其上方为一个 $n$ 行 $m$ 列的网格，其中每一格均为正方形，每一格上面都可以放置障碍物。
我们使用包含两个字母的字符串表示弹珠的运动方向，左上为 LU ，左下为 LD ，右上为 RU ，右下为 RD 。弹珠的运动方向只会是这四种中的其中一种。
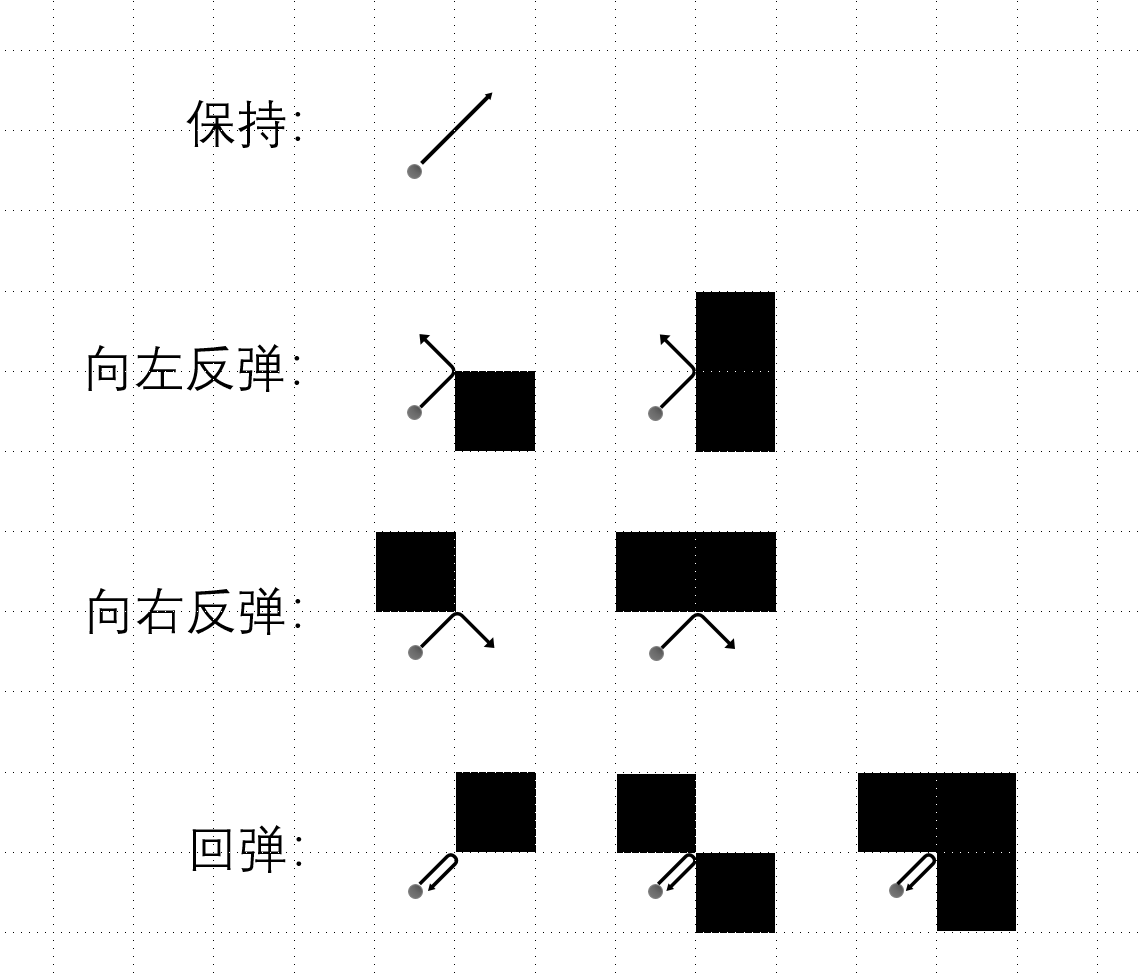
弹珠与弹球桌之间的摩擦力忽略不计，弹珠将从其中一格的中心位置开始，以每秒 $\sqrt{2}$ 格的速率匀速运动。当弹珠运动时如果运动方向的前方、左前方、右前方这三格均没有障碍物，弹珠将保持运动方向继续运动，否则弹珠将在 $0.5$ 秒后碰撞到障碍物，并根据障碍物的位置向不同的方向反弹（如下图）。由于弹珠的半径远小于弹球桌一格的边长，弹珠的半径对弹珠运动的微小影响忽略不计，也就是说我们认为在整数秒时弹珠一定位于某一格的中心位置。
$\texttt{SpadeZ}$ 在布置好弹球桌后， $\texttt{sha7dow}$ 去找他玩弹球桌了！他会在他游玩的第 $0$ 秒发射一颗弹珠，而他发现等待弹珠运动的过程非常漫长，他已经等不及想知道自己的弹珠在 $t$ 秒后会运动到哪一个位置了！给定弹球桌的布局、 $\texttt{sha7dow}$ 的弹珠的初始位置和运动方向，请你计算出他的弹珠在第 $t$ 秒时的位置和运动方向。
输入格式
输入的第一行包含以空格分隔的两个正整数 $n,m$ $(1 \le n \le 500,$ $1 \le m \le 500)$ ，分别表示弹球桌的行数、列数。
接下来 $n$ 行，每行包含一个长度为 $m$ 的字符串，表示弹球桌的布局，左上角的字符位于第一行第一列。其中字符 0 表示这一格有障碍物，字符 . 表示这一格为空位。弹球桌外的位置全部视为障碍物。
接下来一行包含一个正整数 $T$ $(T = 1)$ ，表示来玩 $\texttt{SpadeZ}$ 的弹球桌的同学数量。
接下来 $T$ 行中，第 $i$ $(1 \le i \le T)$ 行包含以空格分隔的三个正整数 $t_i,r_i,c_i$ $(1 \le t_i \le 10^9,$ $1 \le r_i \le n,$ $1 \le c_i \le m)$ 和一个字符串 $dir_i$ ，表示第 $i$ 位同学的弹珠的初始运动状态。其中， $t_i$ 表示弹珠将要运动的时长（单位：秒）， $r_i,c_i$ 表示弹珠的初始行位置、初始列位置， $dir_i$ 表示弹珠初始运动的方向。
保证所有弹珠初始均位于空位。
输出格式
输出 $T$ 行，其中第 $i$ $(1 \le i \le T)$ 行包含以空格分隔的两个整数和一个字符串，表示第 $i$ 位同学的弹珠在运动 $t_i$ 秒后的行位置、列位置、运动方向。
样例
Input
2 5 0.... ...0. 1 7 2 1 LU
Output
1 5 RU
提示
在第一个样例中，弹珠的运动轨迹如下，其中每一个箭头表示一秒：
通知
比赛状态发生变化，点 OK 刷新。
通知