2024年东华大学与昭通学院联合程序设计竞赛

凡凡认为 QQ 飞车有助于 ACM 训练，因为青山哥哥也玩飞车，所以凡凡决定教你玩飞车。

众所周知，在 QQ 飞车中~~（氪金买车、买神宠是最重要的）~~技术是最重要的，没有技术是没有未来的。现在凡凡决定用 QQ 飞车中的一张简单的地图训练你。

这张地图是一张 $n$ 行 $m$ 列（即 $n \times m$ ）的网格图，包含 $n \times m$ 个格点，我们用 $(x, y)$ 表示在第 $x$ 行第 $y$ 列的格点。每个格点都有一个编号，格点 $(x, y)$ 的编号是 $(x - 1) \times m + y$ 。

如图，这是一张 $4 \times 4$ 的网格图：

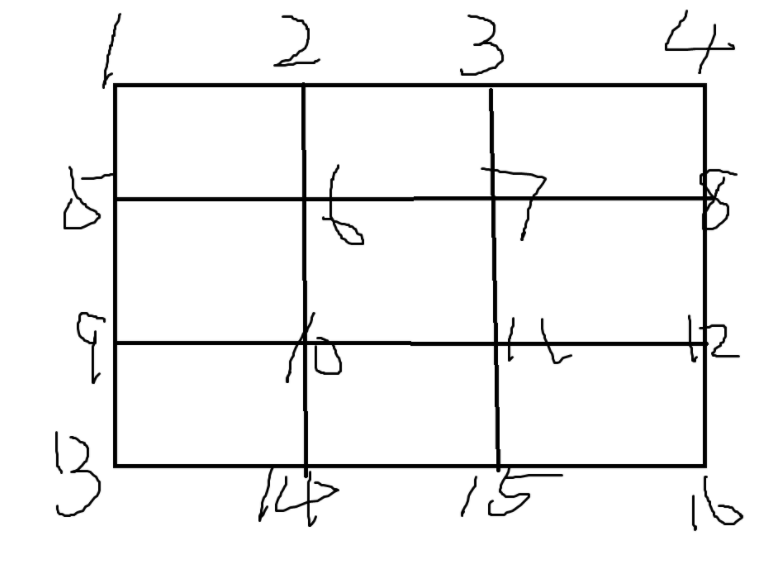
你所驾驶的车只能在格点之间移动，若你在格点 $(x,y)$ 上，那么一次移动可以从移动到四个格点 $(x + 1, y)$ 、$(x - 1, y)$ 、$(x, y + 1)$ 或 $(x, y - 1)$ 中的一个，但不能超出地图。

由于这张图跑法非常的简单，于是凡凡决定给这张图加一些捷径，使其变的复杂。

凡凡会给这张地图加 $q$ 条捷径，每条捷径的两端都是格点且是双向的，用捷径两端格点的编号 $u, v$ 表示这条捷径。设捷径两端的格点是 $(x_u,y_u)$ 和 $(x_v, y_v)$ ，凡凡保证它们一定满足 $x_v =x_u + 1, y_v = y_u + 1 $ 。你可以通过一次移动从 $u$ 号格点到 $v$ 号格点，或者从 $v$ 号格点到 $u$ 号格点。

如图，是在上一张图中的 $5$ 号点和 $10$ 号点之间加一条捷径：

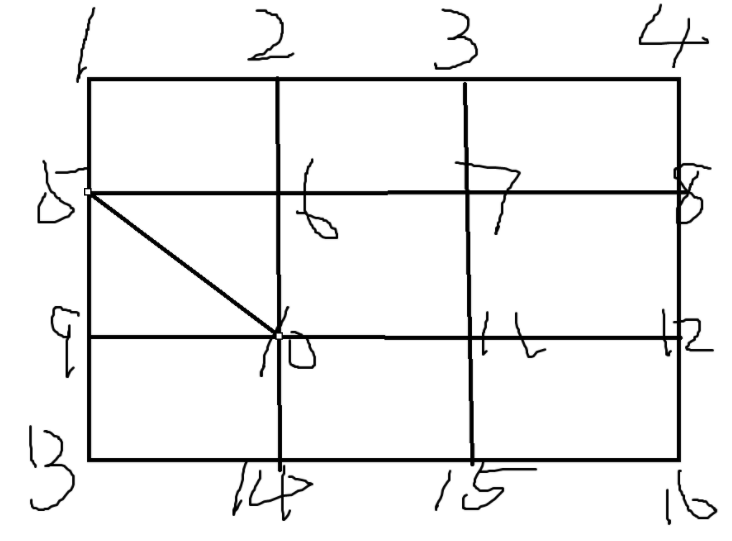
现在，凡凡规定你的起点是编号 $s$ 的格点，而终点是编号 $t$ 的格点。设起点和终点的格点是 $(x_s,y_s)$ 和 $(x_t, y_t)$ ，凡凡保证它们一定满足 $x_s \leq x_t, y_s \leq y_t$ 。你需要回答从编号 $s$ 的格点到编号 $t$ 的格点的最少移动次数。

在第一张图中，从 $5$ 号点到 $11$ 号点最少需要 $3$ 次移动。

在第二张图中，从 $5$ 号点到 $11$ 号点最少需要 $2$ 次移动。