1 人解决，3 人已尝试。
1 份提交通过，共有 8 份提交。
9.9 EMB 奖励。
1460. Dihedral Groups
单点时限: 2.0 sec
内存限制: 256 MB
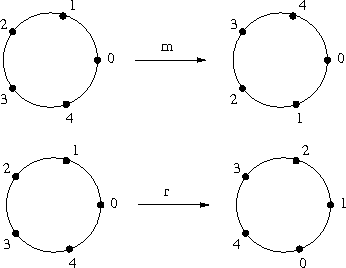
Consider n points on a unit circle with numbers k = 0, 1, …, n − 1. Initially point k makes an angle of 360 ・ k / n degrees to the x-axis, measured in counter-clockwise direction. We are going to perform two different kind of operations on that set of points:
-
rotation by 360 / n degrees in clockwise direction
-
reflection with respect to the x-axis
The following picture shows an example of these operations:
Given a sequence of operations, we are interested in the shortest sequence of operations which gives the same result, i.e., the position of every single point is the same after performing either of those sequences of operations.
The sequence is given as a string consisting of the characters ‘r’ and ‘m’ which represent clockwise rotation and reflection respectively (“to the right” and “mirror”). Multiple consecutive occurrences of the same character are collected into the representation
输入格式
The input file consists of several test cases. Each test case starts with a line containing n (3 ≤ n ≤ 108), the number of points. The second line of each test case consists of an abbreviated sequence of operations as described above. All numbers will be positive and less than 108. There will be no empty line in the input file, and no line will contain more than 100000 characters. The last test case is followed by a line containing 0.
输出格式
For each test case print one line containing the abbreviated format of the sequence with the minimum number of operations which results in the same configuration of points as the input sequence. In case of multiple optimal solutions, print any solution.
样例
Input
4 r2 100 m1 r100 m1 54 r218 m3 r1 0
Output
r2 r1 m1 Hint: Sorry for the Special Judged havn't implemented.
题目标签