2 人解决，2 人已尝试。
2 份提交通过，共有 2 份提交。
7.7 EMB 奖励。
1535. No Rectangles
单点时限: 2.0 sec
内存限制: 256 MB
Consider a grid such as the one shown. We wish to mark k intersections in each of n rows and n columns in such a way that no 4 of the selected intersections form a rectangle with sides parallel to the grid. Thus for k = 2 and n = 3, a possible solution is:
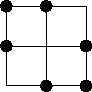
It can easily be shown that for any given value of k, k^2-k+1 is a lower bound on the value of n, and it can be shown further that n need never be larger than this.
Write a program that will find a solution to this problem for k<=32, k-1 will be 0, 1 or prime.
输入格式
Input will consist of some values for k, one of each line. For each value of k, output will consist of n lines of k points indicating the selected points on that line. Print a blank line between two values of k.
输出格式
Input will consist of some values for k, one of each line. For each value of k, output will consist of n lines of k points indicating the selected points on that line. Print a blank line between two values of k.
样例
Input
2 1
Output
1 2 1 3 2 3 1