0 人解决，2 人已尝试。
0 份提交通过，共有 2 份提交。
9.9 EMB 奖励。
1570. Clock Patience
单点时限: 2.0 sec
内存限制: 256 MB
Card sharp Albert (Foxy) Smith is writing a book on patience games. To double check the examples in the book, he is writing programs to find the optimal play of a given deal. The description of Clock Patience reads as follows: ``The cards are dealt out (face down) in a circle, representing a clock, with a pile in each hour position and an extra pile in the centre of the clock. The first card goes face down on one o’clock, the next on two, and so on clockwise from there, with each thirteenth card going to the center of the clock. This results in thirteen piles, with four cards face down in each pile.
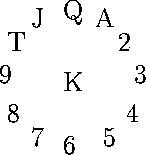
The game then starts. The top card of the king' pile (the last card dealt) is exposed to become the current card. Each move thereafter consists of placing the current card face up beneath the pile corresponding to its value and exposing the top card of that pile as the new current card. Thus if the current card is an Ace it is placed under theone’ pile and the top card of that pile becomes the current card. The game ends when the pile indicated by the current card has no face down cards in it. You win if the entire deck is played out, i.e. exposed.’‘
Write a program that will read in a number of shuffled decks, and play the game.
输入格式
The input will consist of decks of cards arranged in four lines of 13 cards, cards separated by a single blank. Each card is represented by two characters, the first is the rank (A, 2, 3, 4, 5, 6, 7, 8, 9, T, J, Q, K) followed by the suit (H, D, C, S). The input will be terminated by a line consisting of a single #. The deck is listed from bottom to top, so the first card dealt is the last card listed.
The output will consist of one line per deck. Each line will contain the number of cards exposed during the game (2 digits, with a leading zero if necessary), a comma, and the last card exposed (in the format used in the input).
输出格式
The input will consist of decks of cards arranged in four lines of 13 cards, cards separated by a single blank. Each card is represented by two characters, the first is the rank (A, 2, 3, 4, 5, 6, 7, 8, 9, T, J, Q, K) followed by the suit (H, D, C, S). The input will be terminated by a line consisting of a single #. The deck is listed from bottom to top, so the first card dealt is the last card listed.
The output will consist of one line per deck. Each line will contain the number of cards exposed during the game (2 digits, with a leading zero if necessary), a comma, and the last card exposed (in the format used in the input).
样例
Input
TS QC 8S 8D QH 2D 3H KH 9H 2H TH KS KC 9D JH 7H JD 2S QS TD 2C 4H 5H AD 4D 5D 6D 4S 9S 5S 7S JS 8H 3D 8C 3S 4C 6S 9C AS 7C AH 6H KD JC 7D AC 5C TC QD 6C 3C #
Output
44,KD
题目标签