1 人解决，1 人已尝试。
2 份提交通过，共有 3 份提交。
9.1 EMB 奖励。
1656. Click the Lines
单点时限: 10.0 sec
内存限制: 256 MB
In many graphic drawing applications, you can click on a line object. A well-known approach to detect if a line is clicked by a mouse is to compute the distance between the click position and the line. For example, in Figure 1, the line is said to be selected if the distance d is less than a threshold D (d<=D)
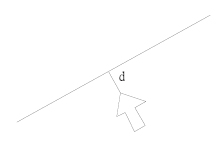
Give you a set of lines (with equation of the form ax + by + c = 0 ), please compute the minimum clicks to select all the lines. For example, to select two lines, the minimum number of clicks is one, that is, you can make a click near the cross point of the two lines.
Note: In the test data, each line at least intersects with another line.
输入格式
The first line of input data begins with a number N - the number of test cases. Each test case begins with two integers L and D , where L (L<=64) is the number of lines and D (D > 0) is the threshold for testing if a line is selected. The data of lines listed one by one. Each line is represented by (ax + by + c = 0) . The three floating numbers a, b, c .. separated by space are given to represent the line.
输出格式
Please output the minimum number of clicks in a new line for each test case.
样例
Input
2 2 5 0 1 0 1 0 0 3 1 0 1 0 1 0 0 1 1 2
Output
1 2 hint: In the data with L >= 12, the lines will have one of the following two properties: Lines are paralized to each other except for less than 5 lines. Lines have a common point of all except for less than 5 lines.
题目标签