10 人解决，28 人已尝试。
11 份提交通过，共有 344 份提交。
7.7 EMB 奖励。
188. 双调巡游
单点时限: 2.0 sec
内存限制: 256 MB
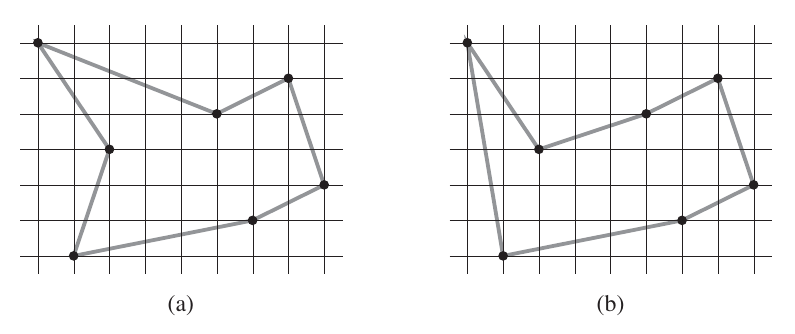
在欧几里得旅行商问题中，给定平面上 $n$ 个点作为输入，希望求出连接所有 $n$ 个点的最短巡游路线。图 (a) 给出了一个 7 点问题的解。此问题是 NP 难问题，因此大家相信它并不存在多项式时间内的求解算法。
J.L.Bentley 建议将问题简化，限制巡游路线为双调巡游 (bitonic tours)，即从最左边的点开始，严格向右前进，直至最右边的点，然后调头严格向左前进，直至回到起始点。图 (b) 给出了相同 7 个点的最短双调巡游路线。问题简化之后，存在一个多项式时间的算法。
输入格式
第一行一个数 $n$，表示共有 $n$ 个点 $(2\leqslant n \leqslant 10^4)$。
接下来 $n$ 行，每行两个整数 $x_i, y_i(|x_i|,|y_i| \leqslant 10^5)$ 表示第 $i$ 个点的坐标（保证 $x_i$ 互不相同）。
输出格式
输出一个浮点数，表示双调巡游距离的最小值。(要求误差不超过 $10^{-3}$)
样例
Input
3 1 1 2 3 3 1
Output
6.47214
Input
4 3 1 4 2 1 1 2 3
Output
788.635e-02
创建: 5 年，12 月前.
修改: 5 年，8 月前.
最后提交: 3 月前.
来源: N/A
题目标签