1 人解决，2 人已尝试。
1 份提交通过，共有 3 份提交。
9.7 EMB 奖励。
1923. Human Knot
单点时限: 2.0 sec
内存限制: 256 MB
A classic ice-breaking exercise is for a group of n people to form a circle and then arbitrarily join hands with one another. This forms a “human knot” since the players’ arms are most likely intertwined. The goal is then to unwind the knot to form a circle of players with no arms crossed.
We now adapt this game to a more general and more abstract setting where the physical constraints of the problem are gone. Suppose we represent the initial knot with a 2-regular graph inscribed in a circle (i.e., we have a graph with n vertices with exactly two edges incident on each vertex). Initially, some edges may cross other edges and this is undesirable. This is the “knot” we wish to unwind.
A “move” involves moving any vertex to a new position on the circle, keeping its edges intact. Our goal is to make the fewest possible moves such that we obtain one n-sided polygon with no edge-crossings remaining.
For example, here is a knot on 4 vertices inscribed in a circle, but two edges cross each other. By moving vertex 4 down to the position between 2 and 3, a graph without edge-crossings emerges. This was achieved in a single move, which is clearly optimal in this case.
输入格式
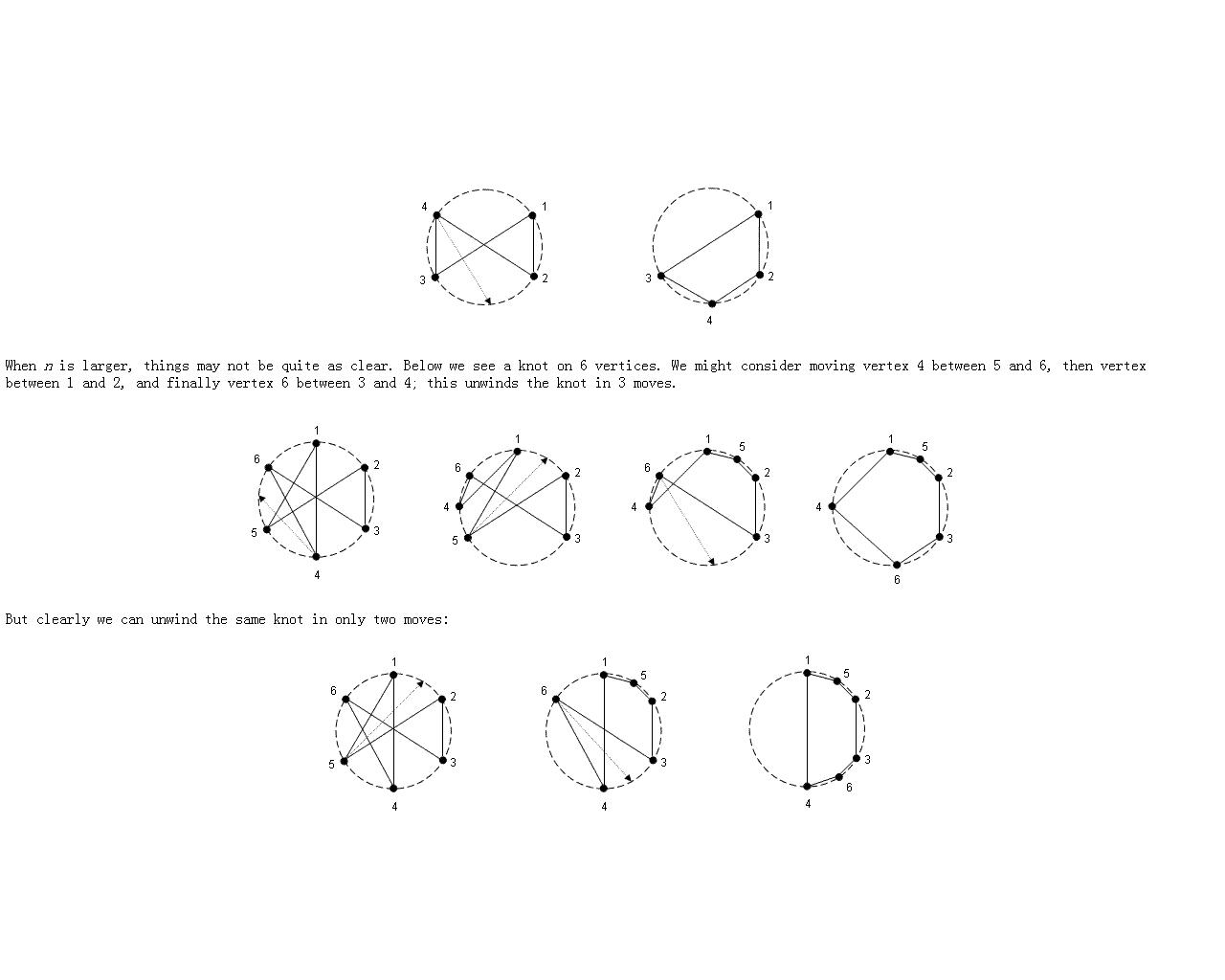
The input consists of a number of cases. Each case starts with a line containing the integer n (3 <= n <= 500), giving the number of vertices of the graph. The vertices are labelled clockwise from 1 to n. Each of the next n lines gives a pair of neighbors, where line i (1 <= i <= n) specifies the two vertices adjacent to vertex i. The input is terminated by n = 0.
输出格式
For each case, if there is no solution, print “Not solvable.” on a line by itself. If there is a solution, print “Knot solvable.” on a line by itself, followed by the minimum number of moves required to solve the problem, on a line by itself.
样例
Input
6 4 5 3 5 2 6 1 6 1 2 3 4 6 2 6 1 4 5 6 2 5 3 4 1 3 0
Output
Knot solvable. 2 Knot solvable. 1
题目标签