14 人解决，47 人已尝试。
17 份提交通过，共有 82 份提交。
7.1 EMB 奖励。
2133. Towers of Hanoi
单点时限: 2.0 sec
内存限制: 256 MB
Everyone is well familiar with the problem of the Towers of Hanoi. Here, you are requires to solve a similar problem. There can be N pegs in all. There are no disks, but a number of balls, each ball has a distinct natural number painted on it. The peculiarity of the balls is that two balls with numbers i and j can remain close to each other if and only if the sum of the numbers on the two balls is a perfect square. Otherwise, they simply push each other from itself with such a force that they can never remain together.
In this problem, you are required to put the maximum possible number of balls on the N pegs, subject to the condition specified above. You have to first place the ball 1, then ball 2, and so on, till no more balls can be put on any of the pegs. The image shown below shows a possible solution for N=4 pegs.
输入格式
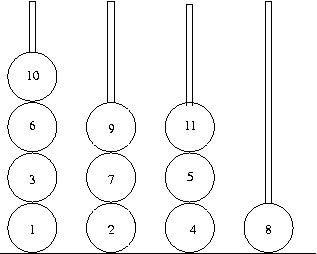
The first line of the input contains K, the number of test cases to follow. Each test case appears on a single line, giving the number N. There are no blank lines or spaces in the input. There will be at most 50 test cases, and 1 <= N <= 50.
输出格式
For each input case, print the maximum number of balls that can be placed on the N pegs. If infinite number of balls can be placed on the pegs, print -1.
样例
Input
2 4 25
Output
11 337
题目标签