137 人解决，190 人已尝试。
251 份提交通过，共有 796 份提交。
3.4 EMB 奖励。
2253. A Knight's Journey
单点时限: 2.0 sec
内存限制: 256 MB
The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular $8 \times 8$ board, but it is still rectangular. Can you help this adventurous knight to make travel plans?
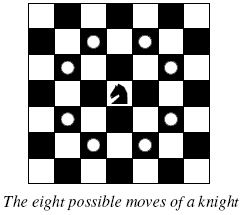
Find a path such that the knight visits every square once. The knight can start and end on any square of the board.
输入格式
The input begins with a positive integer $n$ in the first line. The following lines contain $n$ test cases. Each test case consists of a single line with two positive integers $p$ and $q$, such that $1 \leq p \times q \leq 26$. This represents a $p \times q$ chessboard, where $p$ describes how many different square numbers $1, \ldots, p$ exist, $q$ describes how many different square letters exist. These are the first $q$ letters of the Latin alphabet: $A, \ldots$
输出格式
The output for every scenario begins with a line containing Scenario #i:, where i is the number of the scenario starting at $1$. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number.
If no such path exist, you should output impossible on a single line.
样例
Input
3 1 1 2 3 4 3
Output
Scenario #1: A1 Scenario #2: impossible Scenario #3: A1B3C1A2B4C2A3B1C3A4B2C4
题目标签