2 人解决，3 人已尝试。
2 份提交通过，共有 7 份提交。
8.8 EMB 奖励。
2312. Twirl Around
单点时限: 10.0 sec
内存限制: 256 MB
Let’s think about a bar rotating clockwise as if it were a twirling baton moving on a planar surface surrounded by a polygonal wall (see Figure 1).
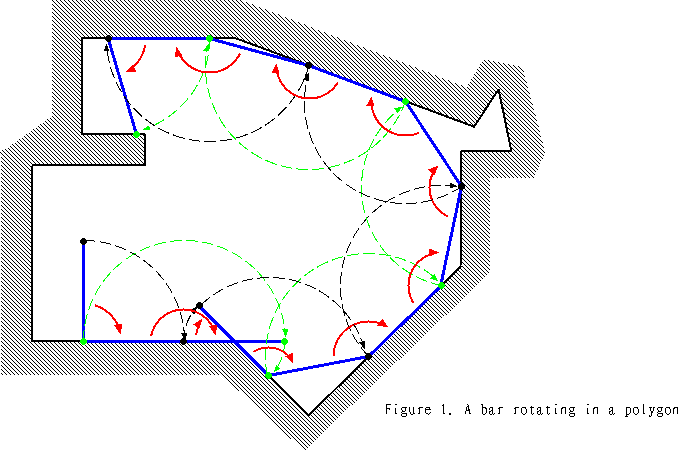
Initially, an end of the bar (called “end A”) is at
The bar turns fixing a touching point as the center. The center changes as a new point touches the wall.
Your task is to calculate the coordinates of the end A when the bar has fully turned by the given count
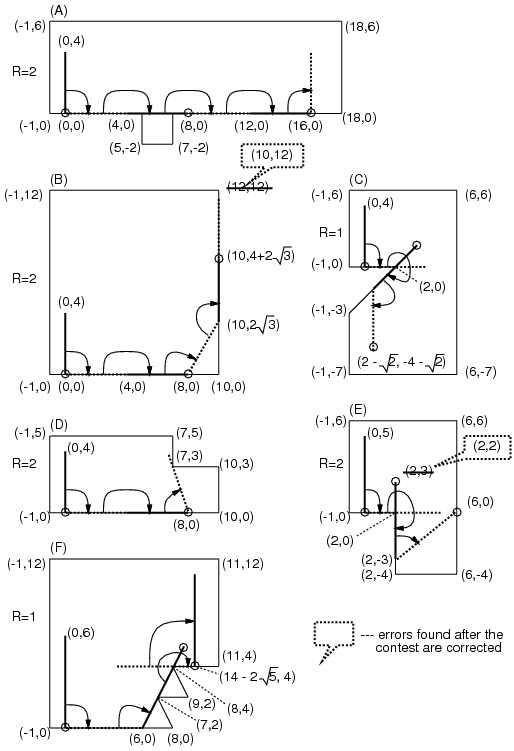
In Figure 2, some examples are shown. In cases (D) and (E), the bar is stuck prematurely (cannot rotate clockwise anymore with any point touching the wall as the center) before
You can assume the following:
When the bar’s length
输入格式
The input consists of multiple datasets. The number of datasets is no more than 100. The end of the input is represented by 0 0 0.
The format of each dataset is as follows:
The vertices of the polygon are arranged in a counter-clockwise order. You may assume that the polygon is simple, that is, its border never crosses or touches itself.
输出格式
For each dataset, print one line containing
样例
Input
4.0 2.0 8 -1 0 5 0 5 -2 7 -2 7 0 18 0 18 6 -1 6 4.0 2.0 4 -1 0 10 0 10 12 -1 12 4.0 1.0 7 -1 0 2 0 -1 -3 -1 -8 6 -8 6 6 -1 6 4.0 2.0 6 -1 0 10 0 10 3 7 3 7 5 -1 5 5.0 2.0 6 -1 0 2 0 2 -4 6 -4 6 6 -1 6 6.0 1.0 8 -1 0 8 0 7 2 9 2 8 4 11 4 11 12 -1 12 0 0 0
Output
16.0 0.0 9.999999999999998 7.4641016151377535 0.585786437626906 -5.414213562373095 8.0 0.0 6.0 0.0 9.52786404500042 4.0 Hint Note that the above sample input corresponds to the cases in Figure 2. For convenience, in Figure 3, we will show an animation and corresponding photographic playback for the case (C).
题目标签