3 人解决，13 人已尝试。
4 份提交通过，共有 59 份提交。
9.3 EMB 奖励。
2478. No Cheating
单点时限: 2.0 sec
内存限制: 256 MB
A local high school is going to hold a final exam in a big classroom. However, some students in this school are always trying to see each other’s answer sheet during exams!
The classroom can be regarded as a rectangle of $M$ rows by $N$ columns of unit squares, where each unit square represents a seat.
The school principal decided to set the following rule to prevent cheating:
Assume a student is able to see his left, right, upper-left, and upper-right neighbors’ answer sheets. The assignment of seats must guarantee that nobody’s answer sheet can be seen by any other student.
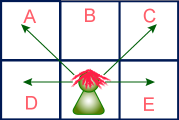
As in this picture, it will not be a good idea to seat anyone in A, C, D, or E because the boy in the back row would be able to see their answer sheets. However, if there is a girl sitting in B, he will not be able to see her answer sheet.
Some seats in the classroom are broken, and we cannot put a student in a broken seat.
The principal asked you to answer the following question: What is the maximum number of students that can be placed in the classroom so that no one can cheat?
输入格式
The first line of input gives the number of cases, $C$ $(C=20)$. $C$ test cases follow. Each case consists of two parts.
The first part is a single line with two integers $M$ $(1 \le M \le 80)$ and $N$ $(1 \le N \le 80)$: The height and width of the rectangular classroom.
The second part will be exactly $M$ lines, with exactly $N$ characters in each of these lines. Each character is either a . (the seat is not broken) or x (the seat is broken, lowercase x).
输出格式
For each test case, output one line containing Case #X: Y, where X is the case number, starting from $1$, and Y is the maximum possible number of students that can take the exam in the classroom.
样例
Input
4 2 3 ... ... 2 3 x.x xxx 2 3 x.x x.x 10 10 ....x..... .......... .......... ..x....... .......... x...x.x... .........x ...x...... ........x. .x...x....
Output
Case #1: 4 Case #2: 1 Case #3: 2 Case #4: 46
题目标签