1 人解决，1 人已尝试。
1 份提交通过，共有 2 份提交。
9.2 EMB 奖励。
2730. The Two Note Rag
单点时限: 2.0 sec
内存限制: 256 MB
Since most computers are binary machines, both powers of two and problems that involve only two values are important to computer scientists. The following problem has to do with powers of two and the digits 1 and 2.
Some powers of two as decimal values, such as 29 = 512 and 289 =
618,970,019,642,690,137,449,562,112 end in a string of digits consisting only of 1’s and 2’s
(12 for 29 and 2112 for 289). In fact, it can be proved that: For every integer R, there exists a power of 2 such that 2K uses only the digits 1 and 2 in its last R digits.
This is shown a bit more clearly in the following table:
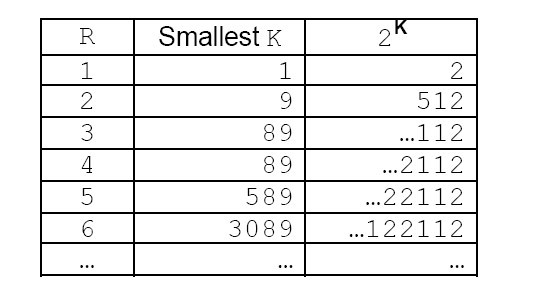
Your job is to write a program that will determine, for given R, the smallest K such that 2K ends in a string of R digits containing only 1’s and 2’s.
输入格式
The first line of the input contains a single decimal integer, N, 1 <= N <= 50, the number of problem data sets to follow. Each data set consists of a single integer R, 1 <= R <= 20, for which we want a power of 2 ending in a string of R 1’s and 2’s.
输出格式
For each data set, you should generate one line of output with the following values: The data set number as a decimal integer (start counting at one), a space, the input value R, another space, and the smallest value K for which 2K ends in a string of R 1’s and 2’s.
样例
Input
6 1 2 4 5 7 15
Output
1 1 1 2 2 9 3 4 89 4 5 589 5 7 3089 6 15 11687815589
题目标签