1 人解决，6 人已尝试。
1 份提交通过，共有 38 份提交。
9.9 EMB 奖励。
2737. Tower
单点时限: 10.0 sec
内存限制: 256 MB
Alan loves to construct the towers of building bricks. His towers consist of many cuboids with square base. All cuboids have the same height h = 1. Alan puts the consecutive cuboids one over another:
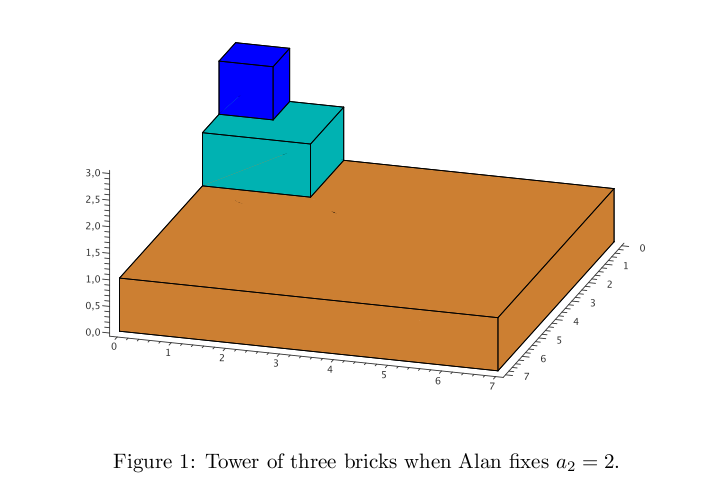
Recently in math class, the concept of volume was introduced to Alan. Consequently, he wants to compute the volume of his tower now. The lengths of cuboids bases (from top to bottom) are constructed by Alan in the following way:
-
Length a1 of the first square is one.
-
Next, Alan fixes the length a2 of the second square.
-
Next, Alan calculates the length an (n > 2) by 2a2an-1-an-2 . Do not ask why he chose such a formula; let us just say that he is a really peculiar young fellow.
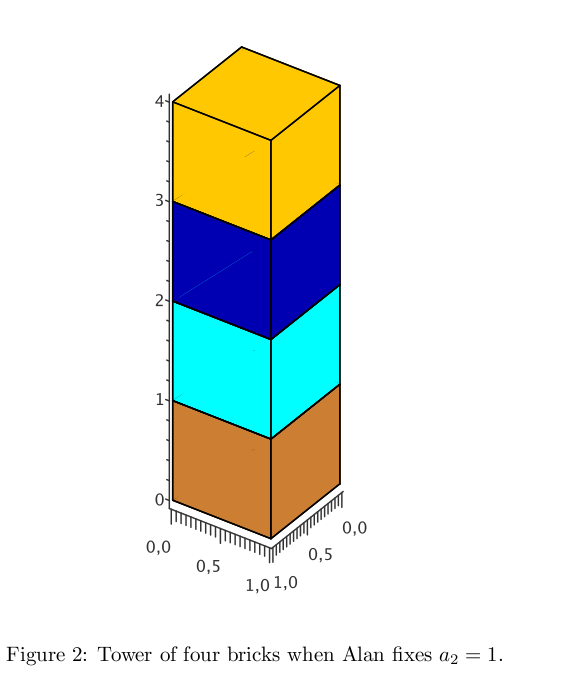
For example, if Alan fixes a2 = 2, then a3 = 8 - a1 = 7; see Figure 1. If Alan fixes a2 = 1, then an = 1 holds for all n ∈ N; see Figure 2.
Now Alan wonders if he can calculate the volume of tower of N consecutive building bricks. Help Alan and write the program that computes this volume. Since it can be quite large, it is enough to compute the answer modulo given natural number m.
输入格式
The input contains several test cases. The first line contains the number t (t ≤ 105 ) denoting the number of test cases. Then t test cases follow. Each of them is given in a separate line containing three integers a2 , N, m (1 ≤ a2 , m ≤ 109 , 2 ≤ N ≤ 109 ) separated by a single space, where a2 denotes the fixed length of second square in step 2, while N denotes the number of bricks constructed by Alan.
输出格式
For each test case (a2, N, m) compute the volume of tower of N consecutive bricks constructed by Alan according to steps (1–3) and output its remainder modulo m.
样例
Input
3 2 3 100 1 4 1000 3 3 1000000000
Output
54 4 299
题目标签