8 人解决，13 人已尝试。
8 份提交通过，共有 34 份提交。
6.9 EMB 奖励。
2750. GCD Determinant
单点时限: 5.0 sec
内存限制: 256 MB
We say that a set S = {x1, x2, …, xn} is factor closed if for any xi ∈ S and any divisor d of xi we have d ∈ S. Let’s build a GCD matrix (S) = (sij), where sij = GCD(xi, xj) – the greatest common divisor of xi and xj. Given the factor closed set S, find the value of the determinant:
输入格式
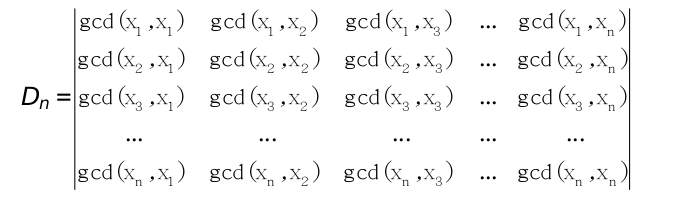
The input file contains several test cases. Each test case starts with an integer n (0 < n < 1000), that stands for the cardinality of S. The next line contains the numbers of S: x1, x2, …, xn. It is known that each xi is an integer, 0 < xi < 2*109. The input data set is correct and ends with an end of file.
输出格式
For each test case find and print the value Dn mod 1000000007.
样例
Input
2 1 2 3 1 3 9 4 1 2 3 6
Output
1 12 4
创建: 15 年前.
修改: 7 年，2 月前.
最后提交: 10 年，9 月前.
题目标签