2 人解决，2 人已尝试。
2 份提交通过，共有 4 份提交。
8.1 EMB 奖励。
2827. Exam
单点时限: 1.0 sec
内存限制: 256 MB
Many universities use scoring system where students can earn up to 100 points, out of which up to 75 — during the semester, and up to 25 — during the final exam. The final mark is determined depending on the sum of semester and examination points by the following table:
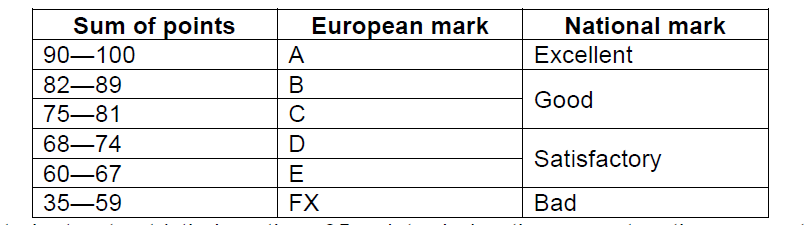
If a student gets strictly less than 35 points during the semester, they are not allowed to pass the examination; let‘s assume in this case that those student‘s names have been excluded from the list.
If you read the column of European marks in examination list from top to bottom, you can find various “words”. For example, if there are consecutive sums of points 92, 75 and 66, they are marked as A, C and E respectively, and form the “word” ACE. In case of FX, both letters (first F, then X) appear in the “word”.
An exam is a risky thing, it‘s impossible to know its results beforehand. But the lecturer knows both the approximate level of knowledge of each student and the list of exam tasks. So the lecturer can estimate the percentage probabilities for each student to earn at the exam every possible number of points: what is the probability that the student gets 0 points, 1 point, …, 25 points – totally 26 nonnegative integers, whose sum equals 100. Points, obtained by every student during the semester, are also known (as fixed numbers from 35 to 75, without any probabilities).
The lecturer is a great esthete and dislikes situations when the “word”, produced by European marks, contains any “unpleasant” substring (just as substring, i.e. when the letters are consecutive).
Your task is to write a program to find the probability that this lecturer the esthete will be satisfied because none of the “unpleasant” substrings will occur.
输入格式
The first line of the input contains the number of test cases. In each test case, the first line contains the number of students $N$ ($3 \le N \le 100$). Each of the following $N$ lines contains $27$ space-separated integers — the number of semester points (from $35$ to $75$), and $26$ probabilities corresponding to $0, 1, 2, \ldots, 25$ examination points (each probability is non-negative, their total sum is $100$). The next line of the test case contains number $K$ ($1 \le K \le 100$) of “unpleasant” words according to lecturer’s opinion. Each of the following $K$ test case lines contains an “unpleasant” word. It’s guaranteed that each of these $K$ lines contains only capital Roman letters (any letters, not only A-F and X). Number of letters in each line is from $2$ to $15$ and it ends with the end-of-line symbol.
输出格式
Your program should write to output exactly one floating-point number in a single line — calculated probability (in percent) that the lecturer will be satisfied. Floating-point format may be any of the standard ones (using decimal point, not decimal comma). The answer will be accepted if its relative error does not exceed $10^{-6}$.
样例
Input
1 3 72 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 2 3 5 7 9 14 16 21 12 5 1 55 0 0 0 1 2 3 4 5 6 7 8 8 9 8 8 7 6 5 4 3 2 2 1 1 0 0 55 0 0 0 1 2 3 4 5 6 7 8 8 9 8 8 7 6 5 4 3 2 2 1 1 0 0 1 DE
Output
79.5
提示
The 1st student‘s sum will be at least 72+10=82 points, so his mark can‘t be D. Thus, “unpleasant” word DE will occur if and only if the 2nd student gets from 13 to 19 points (the probability is 8%+8%+7%+6%+5%+4%+3%=41%) and the 3rd – from 5 to 12 (the probability 3%+4%+5%+6%+7%+8%+8%+9%=50%). So, the word DE will appear with probability 0.41*0.5=0.205, and will not appear with probability 1–0.205=0.795 (i.e. 79.5%).
题目标签