3348. 树的双亲存储法

前面介绍了树的链式存储结构，那么如何用顺序存储来存储一棵树呢？在顺序存储时，我们除了存储每个结点值外，还要存储树中结点与结点之间的逻辑关系（即双亲与孩子结点之间的关系）。下面介绍树的双亲存储法。

1. 编号，从根结点（它的编号为 0）开始，按从上到下的层次顺序，每一层按从左到右的顺序，递增地依次给每一个结点一个编号，图1上标出了各个结点的编号。
2. 存储，如果用一维数组 tree[n] 来存储图1中的这棵树，则树中每个结点存储在 tree[n] 中的下标等于它的编号值，而且在数组 tree[n] 中， 每个元素是一个结构体，它包含两个成员，data 和 parent：其中 tree[i].data 存储一个结点的值， tree[i].parent 存储该结点的双亲结点在该数组中的下标。根结点 tree[O].parent=-1, 图2为图1中树的存储数组。

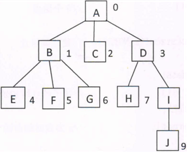
现在给出一棵树的顺序存储结构，打印树的后序遍历。