9 人解决，11 人已尝试。
14 份提交通过，共有 41 份提交。
5.9 EMB 奖励。
3437. 卡车运输
单点时限: 5.0 sec
内存限制: 256 MB
卡车司机运输货物，货物装在集装箱中，集装箱有 26 种不同类型，每种类型的集装箱用一个英文字母表示。卡车容量非常大，能装下任意多的集装箱。
城市里有三种类型道路，司机开过第一种类型道路，则必须将指定类型的集装箱装上车；开过第二种类型道路，则必须将指定类型的集装箱卸下车，否则不能通行，但是司机在卸载时只能卸载最后一个装上车的集装箱；开过第三种类型道路，则不装载也不卸载任何集装箱。
城市有 $n$ 个结点，$e$ 条有向道路。卡车司机从 $1$ 号结点出发，出发时卡车是空的，最后停在 $n$ 号结点，此时卡车上可以有集装箱也可以没有。司机可以重复经过每条道路和每个结点，但他经过的道路总条数不能超过 $k$，请问有多少种合法的路线可供选择？
输入格式
第一行：三个整数 $n$, $e$ 和 $k$。
接下来 $e$ 行，每行首先有两个整数，表示这条道路的起点和终点，如果这条道路是第一种类型的，用一个大写英文字母表示，如果是第二种类型的，用小写英文字母表示，如果是第三种类型的，则没有任何字母。
没有重边和自环。
- 对于 $20\%$ 的数据，满足 $2 \le n \le 5$
- 对于 $100\%$ 的数据，满足 $2 \le n \le 50, 1 \le k \le 50, 1 \le e \le 2450$
输出格式
输出一个整数，表示合法的路线方案数，由于答案可能比较大，输出模 $10007$ 的余数。
样例
Input
2 1 10 1 2 a
Output
0
Input
7 9 5 1 2 A 2 3 B 2 5 5 3 C 3 4 b 3 6 c 3 7 4 7 a 6 7 a
Output
4
提示
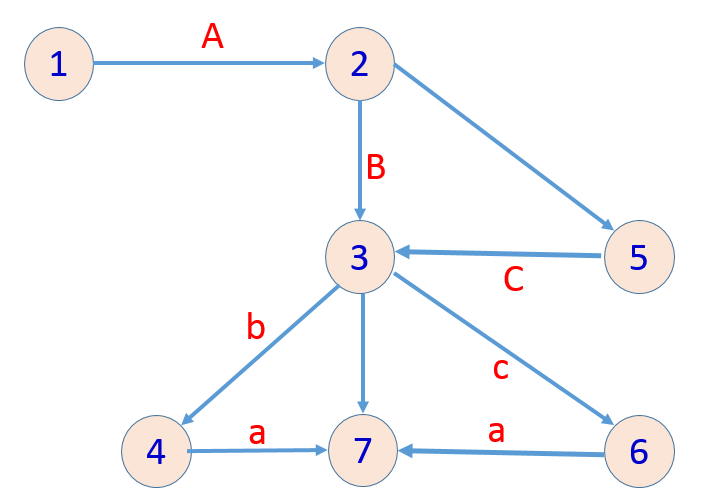
可能会重复经过同一个结点。
四种路线方案：
1->2->3->7
1->2->3->4->7
1->2->5->3->6->7
1->2->5->3->7