2018 ECNU One,Two,Three,AK's ICPC/CCPC Training Contest
2018 ECNU One,Two,Three,AK's ICPC/CCPC Training Contest
Date
2018.10.04
Comment
由于是互鏼,没有用整套题目,重组了一部分我们训练中遇到的好题,所以大部分题目的难度集中在mid左右(银牌题到金牌题之间)。可能比赛不会有区分度,但都是值得尝试与思考的题目,赛后把这些题目都补了,一定会有收获!
前期题目比较坑,可能会打到自闭,但是可以感受一下现场赛卡题的感觉。
题目来源以及难度
A 2017 CCPC-Final HDU 6250 hard
B 2017 广西邀请赛 HDU 6191 mid
C 2008 NEERC 某预选赛 URAL 1651 mid easy
D 2008 NEERC 某预选赛 URAL 1658 mid easy
E 2008 NEERC 某预选赛 URAL 1650 mid easy
F 2015 多校训练6 HDU 5355 mid
G 2013 南京邀请赛 HDU 4587 mid
H 2013 南京邀请赛 HDU 4586 easy
I NEERC12 GYM 100134C mid easy
J NEERC12 GYM 100134J mid
K NEERC11 GYM 100085D mid hard
L NEERC11 GYM 100085L hard
M atcoder AtCoder 2165 mid hard
补题建议
预计铜牌队伍最终在2到4题左右,银牌队伍做出所有的mid easy以及一个mid(5到6题左右),金牌队伍做出至少7题。
mid easy 对应于铜牌题难度,如果mid easy一个都不会做那可能要自费了,mid easy都过了那可能到银牌区了。
mid 对应银牌题难度。
mid hard 对应金牌题难度。
hard 现场赛应该不会到两位数的ac。
建议铜牌队伍除了补完所有mid easy以外,补一下B和G。
Problem A
算法:高斯消元,高等代数&解析几何
难度:mid hard
题意:给定$m$个$n$维的点,两两之间距离为1,求最多能加多少个点保证这一性质,并输出坐标。
题解:考虑从$m$个点加新的一个点的情况,只需要找到$m$个点所在的$m-1$维平面上的中心以及法向量,可以找规律发现新加的点离$m$维平面的距离为$\sqrt{\frac{m + 1}{2 * m}}$
中心非常好求,法向量则可以通过两点之间的中垂面(高维中不知道叫什么)的交线来确定,这个可以利用高斯消元求出来(没用的维数用1来代替,最后乘以距离的权重就可以)。
oxx列的方程是 $(\vec{p_{i + 1}} - \vec{p_{i}}) \times \vec{x} ^ {T} = 0$ ($p$是已添加的点,由于方程个数少于未知数,将未知数后若干位直接标为1就可以求出确定的向量了,这样目的是防止退化成全0解)。
Problem B
算法:01trie,离线启发式合并/dfs序/在线可持久化trie。
难度:mid
题意:给一棵树,每个节点有个权值。若干次查询,每次查询一棵子树中的数与一个数异或最大为多少。
题解:查异或最大是典型01trie,关键是如何在一棵子树中计算。
这题有很多解法,离线可以启发式合并,也可以dfs序做(类似校赛的C)。
在线可以可持久化trie,类似主席树写法,不会的建议补一下。
Problem C
算法:最短路/dp
难度:mid easy
题意:给出一条链,求链上边的子集,使得起点到终点了联通。
题解:绝对的自闭题。
对于每一个点的不同次访问,把每个点拆开了,对于访问次数不同但是一样的点,两两连边权为0的边,然后从起点到终点跑最短路就行了。
另也可以按顺序dp,但是注意记录路径时不能按值记录,而是要记录标号(第几个读入),否则会导致后面的覆盖前面的值。
几种错误姿势:
错误一:bfs,显然错误,没读清题,要按边的顺序,bfs相当于无视条件2。
错误二:消环,显然错误,1 2 3 1 4 2 5,答案应该为1 2 5,消环会错误消去1 2 3,结果变为1 4 2 5
错误三:路径输出错误
Problem D
算法:dp
难度:mid easy
题意:给出一个数的数字和以及数字的平方和,求最小满足题意的数。
题解:内存卡的很紧。
用$f[I][j]$表示$s1$位$i$和$s2$为$j$的最小值
显然位数位$100$是存不下的,我们就存当前位置,然后递归一下,把每一位的答案拿出来,排个序,从小到大输出即可。
此题的关键点在于长度相同时应该如何选取,显然无法将整个路径存下判断,但是我们可以得到的结论是一定取让最小数尽量小的方案。
因此在从小往大的dp,就要小于等于更新,从大往小的dp(记忆化搜索),就要严格小于更新。
正确性就是这样能保证最小数的最小。
Problem E
算法:模拟,stl/线段树
难度:mid easy
题意:给一堆百万富翁,每个人在某个城市,某些时刻会某些富翁会移动所在的城市。求最后所有城市在多少天为最有钱的城市。
题解:按题意模拟一下即可,用set或者线段树维护最大值都可以。注意边界以及先后顺序。有个可能的坑点就是没说百万富翁一定是一百万的倍数,所以必须LL存。
Problem F
算法:暴力,构造
难度:mid
题意:把$1-n$这$n$个数,分成$m$堆,使得$m$堆数的和相等。
题解:首先考虑没有解的情况。
显然,没有解的无非是$n$无法整除$m$,或者是$\frac{n}{m}<n$(即最大的一个数无法放入任何一组)
将较大的数,每$2\times m$为一组,放入$m$堆中,从小到大相应配对,显然和相等
当剩下的数不足$3\times m$个时,直接暴力dfs配对即可。
选拔赛第三场C的强化版,认真想过这个问题的应该很快能秒。
Problem G
算法:tarjan
难度:mid
题意:给一个无向图,求删掉两个点之后最多联通块数量。
题解:枚举一个点,剩下的tarjan判割点,判割点时,每当其被判为割点(某个儿子下的反边不高于其,具体需要理解tarjan),那么联通块加一。
需要理解tarjan算法才能做此题。
Problem H
算法:签到
难度:概率
题意:给定一个骰子,有若干个面,当掷到某个面得到一定的钱。某些面可以再掷一次,问掷一次获得钱的期望
题解:直接算一下即可,注意和为0,$n$ 等于 $m$ 的情况,答案为0。
Problem I
算法:二分答案(非正解)
难度:mid easy
题意:给每个人分配一个相同的长度,使得每个人可以在自己的区间里面找出互不重叠的区间。
题解:用 long double 来二分答案,然后暴力枚举分母,找出分数的表示。这种做法需要注意优雅的化小数为分数的姿势。
Xiejiadong:当时就是调精度调自闭了。
Problem J
算法:构造
难度:mid
题意:从0出发,用$a$次$\pm 1$,$b$次$\pm 2$,$c$次$\pm 3$遍历所有的$0$到$a+b+c$点。
题解:先把$c$次$\pm 3$的处理掉。我们通过向右、向左、再向右三部分,把前面的一部分填满,并且最后填的一个的左边已经全部填满,右边全部没有填过
再向右一步一步填,剩下一个$\pm 1$用来在最后改变方向,剩下的$\pm 2$我们用过向右、转弯、向左来填满右边剩下的部分
注意各类情况的处理与细节问题
Problem K
算法:Trie树
难度:mid hard
题意:可以将两个字符串首位相接,或者取单个字符串,求本质不同的字符串有几个。
题解:用Trie树来跑,按照前缀和后缀分别构建Trie树,显然这样做是会重复的。
而重复的一段必然是由于中间段相同所引起的。那么我们可以处理前缀的后缀和后缀的前缀相同的个数,用类似于二元容斥的方法来判重。
Problem L
算法:想法
难度:hard
题意:有一座桥,从左往右有$n_1$条路,从右往左$n_2$条路,有一条路为待定。即早上有$(n_1+1)$条从左往右,晚上有$(n_2+1)$条从右往左,路改变方向需要等r个时刻。分别告诉你从1到m时刻的两个方向车数量。要求决定一个时刻改道路方向,使得所有车辆等待时间最小化。
题解:左往右与右往左是两个独立的问题,设$f[i]$表示i时刻开始左从右车道减少一条的答案。容易发现$f[i]$与$f[i + 1]$是有关系的。所以线性计算。首先计算出来$f[m+1]$即从左往右都是$(n_1+1)$,来开始减少车道。若从$(n_1+1)$减少到$n_1$,如果原来该时刻通过车辆少于$(n_1+1)$,那么什么都不做。否则说明有一辆车此时通过不了,需要找到后面最早有空余车道的时刻让其通过,这个只需要队列记录一下。所以可以$O(1)$转移。同理从右往左。
Problem M
算法:二分答案+思想
难度:hard
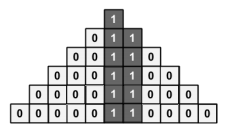
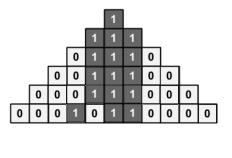
题意:每层每个格子里的数为其下方三个数的中位数,给出底层的数,求顶层的数。
题解:考虑二分答案,假设当前需要验证的答案为$x$,表示答案$≥x$是否成立
那么,根据最下面一行和$≥x$的关系,我们可以得到底层的$0/1$数列,$1$表示$≥x$
我们现在得到了底层的$0/1$数列,而题目所给的条件,上一层的一格为$1$,当且仅当下一层与之对应的三个中至少有两个$1$
现在,符合情况的话,那么就是顶层为$1$
我们可以画画图来分析一下底层的情况,如何向上传导
我们可以发现,当出现连续的两个$1$的时候,他们所对应的的上面,全部为$1$
那么,这样的情况如何向外拓展呢?
我们发现,当连续的两个$1$旁边出现隔着一个位置的$1$的是否,这个全是$1$的竖行,可以向着隔着一个位置的$1$的方向拓展一列
那么我们只需要正着反着,各扫一遍
这样一来,我们就可以在$O(2n)$的时间内验证答案了
还有一种比较特殊的情况是,底层不需要出现连续的两个$1$
特判一下
总的时间复杂度是$O(3n\times logn)$