2018 Multi-University, Nowcoder Day 4
Problem A
Solved by zerol. 02:17 (+2)
题意:给一个 012 的字符串,每过一个单位时间 1->10, 2->21 并且移除第一个字符。问最后变成空串会需要多少时间。
题解:写个递推式(大概很简单?),发现需要对 2 递归地取幂。于是需要模欧拉函数,并考虑到 a 和 p 不互素的情况,需要使用——当 $x \ge \phi(p)$ 时有 $a^x \equiv a^{x \; mod \; \phi(p) + \phi(p)} \pmod p$。但是需要判断 $x$ 和 $\phi(p)$ 的大小关系,所以对 x 绑一个 double,参与除了取模外的一切运算,然后就能愉快地比大小了。
ultmaster: 有关递推式是怎么写出来的:比如说考虑一个 2 被消掉,或者被放着 1 步不管、2 步不管……最后消掉的情况。那么在前面还没消完的情况下,后面是可以自由增长的,直到这个罪恶的根源暴露在第一个被吃掉了。剩下的就打个表(真的很简单)。
Problem B
Upsolved by ultmaster.
题意:给若干个带权区间,每个带权区间的功能是给一段区间给的数都加一个权。现在要求在所有数都被覆盖到的情况下,最大数的最小值。
题解:一个很显然的观察是同一个数不能被三个及以上区间覆盖。(证明:取一个覆盖到最右端的,取一个覆盖到最左端的,那么至多两个,多的肯定可以删掉)
DP 状态 $f(i,j)$ 表示当前末端选的是 $i$,上一次和别人重叠的地方是 $j$,上一次和别人重叠的地方的最小厚度。那么,按右端点排序后有:$f(i,r_k) = \min_{r_k \ge l_i - 1, x < l_i}(f(i,r_k), \max(f(k,x),w_i+w_k))$。当 $i$ 区间和 $k$ 区间不相交时,$w_i+w_k$ 应该改成 $w_k$。这个用一个类似前缀和的最小值优化就可以(根本就不是题解所说的线段树,用线段树可能可以做到更高的数量级)。答案 $ans = \min_{r_i=m,0 \le j \le m} ( \max(f(i,j), w_i) )$。
边界处理的话,我增加了一个免费的 $(0,0)$ 区间放在最前面。
Problem C
Solved by ultmaster. 02:57 (+1)
题意:[math]\displaystyle{ a_n = \begin{cases} 0 & n = 1, \\ a_{\lfloor \frac{n}{2} \rfloor } + (-1)^{n(n+1)/2} & n \ge 2 \end{cases} }[/math],求 $\sum_{i=1}^n |a_i|$。
题解:$a_n$ 只跟其二进制上每相邻两位组成的数(0 或 1 或 2 或 3)有关。所以数位 DP 即可。数组开小了改了半天。。。。
另解 (by oxx): 发现写在一个二叉树里以后,数目刚好成一个杨辉三角。然后随便算算。
Problem D
Solved by zerol. 01:19 (+1)
题意:构造一个 0, -1, 1 的 $n\times n$ 矩阵,使得每行每列数之和共 2n 个数互不相同。
题解:发现对于偶数的构造方式并猜想对于奇数无解。对于 n=2 样例中给出了解。对于 n=大于 2 的偶数,将其分解为两个偶数 a+b,对于左上 a*a 和右下 b*b 递归求解,剩下部分右上按照一行 1 一行 -1 交替填,左下按一列 1 一列 -1 交替填。
Problem E
Upsolved by kblack.
题意:一堆概率出现的点,求在任意点左下角的点数的期望。
题解:记录不在任意点左下角的概率,每个点相当于对一个矩形乘以 $(1-p)$,扫描线+线段树即可。
Problem F
Solved by ultmaster. 00:37 (+)
签到。读错了好多次题。在队友的搀扶下艰难地过了。
Problem G
Solved by kblack. 00:39 (+)
枚举即可,温暖的规律签到。
Problem H
Upsolved by kblack.
题意:给一个长长的字符串 $s$,问有多少对 $(i, j) 1 \leq i < j \leq n$ 使得交换 $s_i$ 和 $s_j$ 之后,原串可以拆成两个回文串。
题解:首先不考虑交换两个相同的字符,枚举拆开的位置,分别判断两边需要怎么操作才能变成回文串,可以 Hash 或使用后缀技术,然后按两边的情况分类讨论,就可以得到交换方式了。因为每个切开位置最多产生 4 个交换方式,交换方式数量 $O(n)$,set 去重即可。过程中可以知道,是否不用交换原串也能拆成两个,如果能,统计一下每个字符的数量算一算就好了。
kblack: 分类讨论烦得一批,即使当时意识到了交换不同字符的方式是 $O(n)$,也大概率调不对吧。
Problem I
Upsolved by ultmaster.
题意:给出 $n$ 对三元组 $(a_i, b_i, c_i)$,保证 $3n$ 个数互不不相同且在 $1$ 到 $3n$ 之内。构造⼀个排列使得 $b_i$, $c_i$ 出现在 $a_i$ 后⾯,并且 $\sum |p_i - p_{i-1}|$ 最⼩。
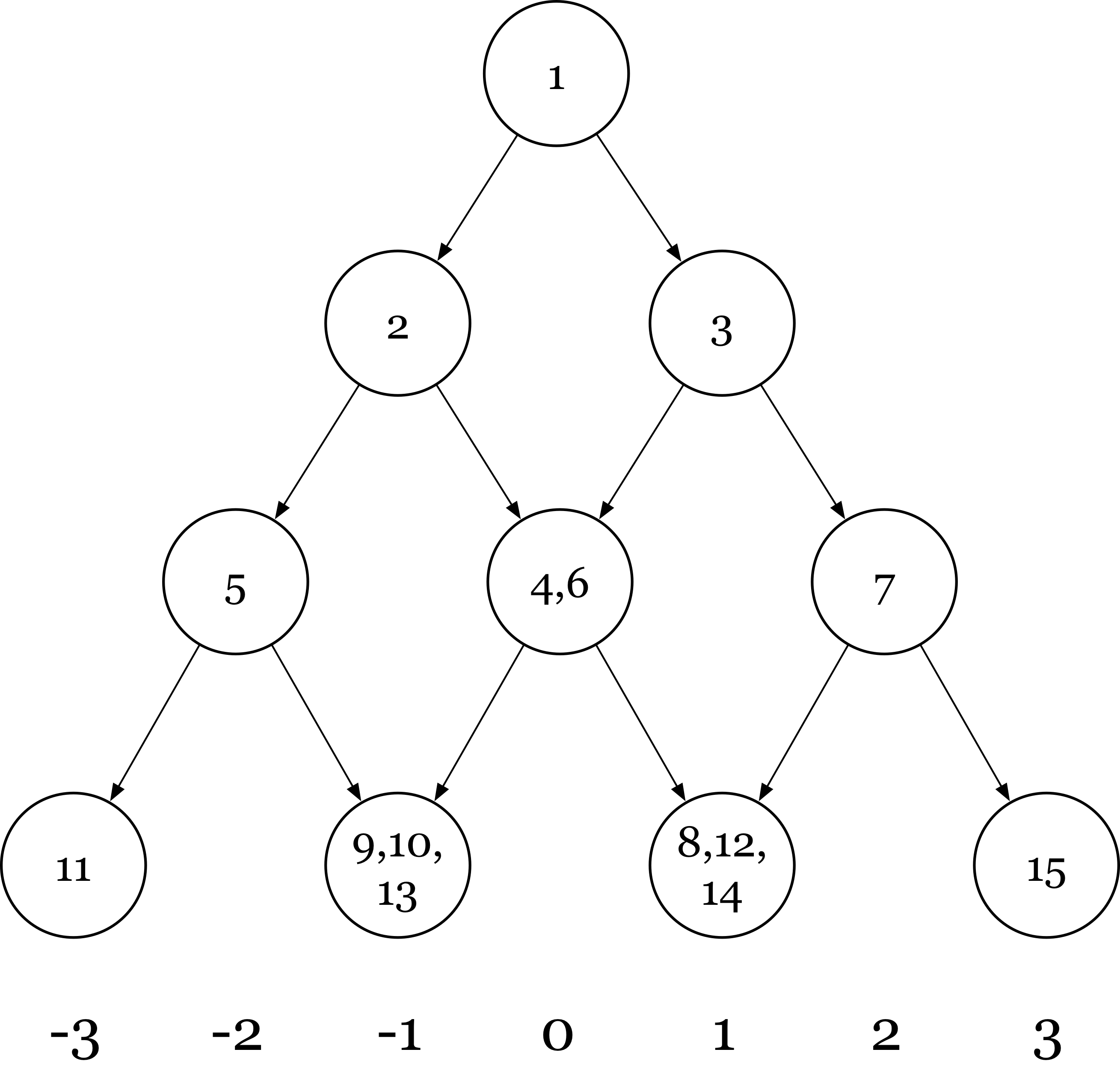
题解:(基本照抄题解) 其实是在 $1$ 到 $3n$ 的数轴找一条最短路。一个显然(不显然)的 observation 是:同一个点不能经过超过三次。所以肯定是下面两张形态:
然后根据题解的说法,直接 DP 就好了。(然而,这个 DP 似乎并不显然。。。
我们研究什么地方需要走两次,或者三次。我们根据三元组的依赖关系,就拿到了一系列的 $(b_i, a_i), (c_i, a_i)$ 这样的区间,这些区间是可能要走两次的。用扫描线的方法合并掉相邻的。剩下的区间一定是不相交的。我们记为区间:$(l_1, r_1), (l_2,r_2), \ldots, (l_m,r_m)$。
不考虑边界的话,我们要求的就是 $\min_{1 \le j < k \le m} \left( (r_j - 1) + \sum_{i=j+1}^{k-1} 2(r_i - l_i) + (3n - l_k) \right)$。这个东西用 DP 扫一遍就可以解决。剩下的事情就是处理边界:我的方法是在前面增加一个区间 $(1,1)$,后面增加一个 $(3n, 3n)$。此题还需要输出方案,所以取 $\min$ 的时候要顺带记录下标。输出方案的话,模拟一下就好了。
哦对了还有反过来的情况,把所有的数都置成 $3n-x+1$ 就好啦。
Problem J
Solved by kblack. 04:05 (+8)
题意:naive 的 hash 函数,naive 的解决方法(往后放),给出结果,求字典序最小的原插入顺序。
题解:很明显的拓扑排序,原题解是线段树优化。也可以考察特殊条件,所有相交的区间合并,包含的区间只会被跳一次,瞎几把搞一搞就好了,注意无解的判断即可。
zerol:
另解1:大约 40 行远小于 200 行。用并查集维护从位置 p 开始下一个还没有放的位置。一开始将所有能直接放的数及其位置放入优先队列,每次选区数字最小的放,然后更新并查级中它的后继,检查后继是否能放,如果能则放入优先队列。
另解2:大约 80 行远小于 200 行。线段树上建图。代价就是点数 *4,对于线段树上的点一开始 o 依赖 lc(o) & rc(o),其他依赖关系按题意,然后开个优先队列求拓扑序。