2020 年 “联想杯”全国高校程序设计在线邀请赛暨第三届上海理工大学程序设计竞赛
单点时限: 1.0 sec
内存限制: 256 MB
On the magical land Byteland, there is an ancient kingdom called Fibonacci Kingdom.
There are $n$ cities in the kingdom(numbered from $1$ to $n$), and $\text{Fib}_i$ residents in the $i$-th city.
$\text{Fib}_i$ denotes the $i$-th number of Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from $1$ and $1$. That is, $\text{Fib}_0=1,\text{Fib}_1=1$ and $\text{Fib}_n=\text{Fib}_{n-1}+\text{Fib}_{n-2}$ for $n>1$. The beginning of the sequence is thus: $1,1,2,3,5,8,13,21,34,55,89,144,\cdots$.
Unfortunately, one day, an earthquake occurred.
The earthquake destroyed the whole kingdom’s transportation system.
To deliver disaster relief supplies, the king decided to reconstruct the road.
$m$ plans have been proposed, and the $i$-th plan is to reconstruct the bidirectional road linking $x_i$ and $y_i$, denoted as $(x_i,y_i)$.
The magic is that it takes exactly $\text{Fib}_{x_i}+\text{Fib}_{y_i}$ bitcoins to reconstruct the road $(x_i,y_i)$.
The king wants to choose some plans to implement, but the rules below must be followed:
- After the reconstruction, the cities are mutually reachable (i.e., there is at least one path connecting any two cities).
- Minimize the bitcoin consumption.
- In the premise of the least bitcoin consumption, the largest degree $D$ among all the cities should be minimized(suppose $d_i$ is the degree of $i$-th city, $D=\max\limits_{1\leq i \leq n} d_i$), because the residents of the kingdom are not good at looking for ways. The definition of the degree of a city is the number of roads directly connected to the city.
Setsuna, the savior of the kingdom, has easily calculated the minimum consumption of bitcoin, but she desperately wants to know the minimum $D$ she can get after reconstruction.
It’s guaranteed that the answer always exists.
输入格式
The first line contains two integers $n,m(2 \leq n \leq 10^5, n-1 \leq m \leq \min(\frac{n\times(n-1)}{2},2 \times 10^5))$.
The $i$-th of the next $m$ lines contains two integers $x_i,y_i(1 \leq x_i,y_i \leq n,x_i \neq y_i)$.
输出格式
Output one integer which indicates the minimum $D$ Setsuna can get.
样例
5 6 2 1 2 4 1 3 3 4 4 5 1 5
3
提示
The graph of the sample is as follows.
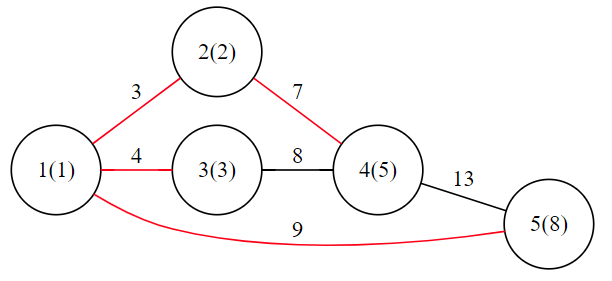
In this situation, bitcoin consumption is $3+4+7+9=23$. The degree of city $1$ is $3$; the degree of city $2$ is $2$; the degree of city $3,4,5$ is $1$.
It can be proved that such solution is the best, so the answer is $3$.