2020 年 “联想杯”全国高校程序设计在线邀请赛暨第三届上海理工大学程序设计竞赛
单点时限: 1.0 sec
内存限制: 256 MB
The beautiful campus of University of Shanghai for Science and Technology is lined with trees. It takes ten years to grow trees and a hundred years to nurture talents. The trees have witnessed the growth of generations. Unconsciously, the season of graduation has quietly arrived.

To commemorate the contributions of seniors to the algorithm contest of University of Shanghai for Science and Technology, everyone decides to plant an unrooted tree of $n$ vertices in the school. Vertices are numbered from $1$ to $n$.
It’s difficult to satisfy everyone’s aesthetic, so the tree should meet some constraints.
There are $m$ constraints of type $1$ and $k$ constraints of type $2$.
The $i$-th constraint of type $1$ can be represented by a pair $(x_i,y_i)$, which indicates there should be an edge connecting vertex $x_i$ and vertex $y_i$.
The $i$-th constraint of type $2$ can be represented by a triple $(op_i,x_i,deg_i)$. $op_i$ indicates the type of the restriction, $1$ for the upper limit and $0$ for the lower limit. $x_i$ indicates the number of the vertex. $deg_i$ indicates the extreme value of degree of vertex $x_i$.
For example, the constraint triple $(1,3,1)$ means that the degree of vertex $3$ should be at most $1$, and the constraint triple $(0,1,2)$ means that the degree of vertex $1$ should be at least $2$.
You need to count how many kinds of trees meet all constraints simultaneously. Notice that the answer might be very large, so please output the desired answer modulo $998244353$.
There are some definitions you may need to know: an undirected connected graph is a tree if and only if it has $n$ vertices and $n-1$ edges; two trees are considered different if and only if their adjacency matrixes are different.
输入格式
The first line contains three integers $n,m,k(2 \leq n \leq 60, 0 \leq m \leq n-1,0 \leq k \leq 60)$.
The $i$-th of the next $m$ lines contains two integers $x_i,y_i(1 \leq x_i,y_i \leq n,x_i \neq y_i)$.
The $i$-th of the next $k$ lines contains three integers $op_i,x_i,deg_i(0 \leq op_i \leq 1,1 \leq x_i \leq n,0 \leq deg_i < n)$.
输出格式
Output one integer in a single line.
样例
4 3 1 1 2 2 1 1 2 1 1 1
3
4 3 1 1 2 2 3 1 4 0 1 2
1
4 3 0 1 2 2 3 3 1
0
提示
In sample $1$, there are $3$ trees that meet all constraints.

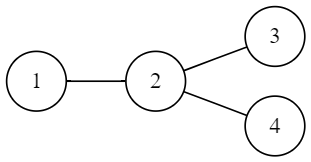

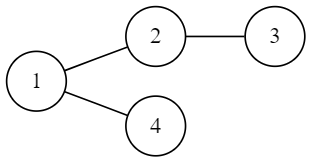
In sample $2$, there is only $1$ tree that meets all constraints.
In sample $3$, there is no tree that simultaneously meets all constraints.