2020 年 “联想杯”全国高校程序设计在线邀请赛暨第三届上海理工大学程序设计竞赛
单点时限: 1.0 sec
内存限制: 256 MB
This is an interactive problem.
As we all know, JXC is the red sun of USST. Now, he is going to play an easy game with Setsuna.
Setsuna is given a grid $n \times m$. Rows are enumerated from 1 to $n$ from up to down, and columns are enumerated from $1$ to $m$ from left to right. Cell, standing on the intersection of row $x$ and column $y$, is denoted by $(x,y)$, and the number in cell $(x,y)$ is denoted as $A_{x,y}$.
Every cell contains $0$ or $1$, but only JXC knows what they are.
Setsuna wants to know numbers in all cells of the grid. To do so we can ask the following questions:
- ”$?\ x_1\ y_1\ x_2\ y_2$”, where $1 \leq x_1 < x_2 \leq n,1 \leq y_1 < y_2 \leq m$. Setsuna can get the number of good pairs in the submatrix with $(x_1,y_1)$ as the upper left corner and $(x_2,y_2)$ as the lower right corner through this query. Obviously, the size of the submatrix she will output is not smaller than $2 \times 2$. Good pair is the adjacent pair with the same value. Formally, it is an unordered pair $((x_1,y_1),(x_2,y_2))$ which satisfies both $|x1-x2|+|y1-y2|=1$ and $A_{x_1,y_1}=A_{x_2,y_2}$.
- ”$?\ x\ y$”, where $1 \leq x \leq n,1 \leq y \leq m$. Setsuna can get the number in cell $(x,y)$. She can perform no more than 5 queries of this type.
For example, for the graph below, answer for “? $1\ 1\ 3\ 3$” is $4$ and answer for “$?\ 3\ 4$” is $0$.

You are required to help Setsuna to determine all cells of the grid by asking not more than $2000$ questions(including two kinds of questions and the guess of the answer). It can be shown that the answer always exists.
交互流程
The first line contains two integers $n,m(3 \leq n,m \leq 32)$.
Interaction Protocol
You begin the interaction by reading $n,m$.
To ask a question about submatrix $(x_1,y_1),(x_2,y_2)$, output “$?\ x_1\ y_1\ x_2\ y_2$” in a separate line.
Numbers in the query have to satisfy $1 \leq x_1 < x_2 \leq n$ and $1 \leq y_1 < y_2 \leq m$.
To ask a question about the number in cell $(x,y)$, line output “$?\ x\ y$” in a separate line.
Numbers in the query have to satisfy $1 \leq x \leq n$ and $1 \leq y \leq m$.
Don’t forget to ‘flush’, to get the answer.
In response, you will receive the number of good pairs if you asked the submatrix or the number in the cell otherwise.
In case your query was invalid or you asked more than $2000$ queries(including two kinds of questions and the guess of the answer) or you asked more than $5$ queries of the second type, program would print $−1$ and would finish interaction. You would receive Wrong answer verdict. Make sure to exit immediately to avoid getting other verdicts.
When you determine numbers in all cells, output “$!$”. There must be a line break(‘\n’) after “$!$”.
Then output $n$ lines, the $i$-th of which is a string of length $m$, corresponding to numbers in the $i$-th row of the grid.
Note that you have only $1$ chance to guess the answer, and after outputting the answer, your program must be terminated immediately without outputting anything.
After printing a query, do not forget to output end of line and flush the output. Otherwise, you will get Idleness limit exceeded. To do this, use:
- $\text{fflush(stdout)}$ or $\text{cout.flush()}$ in C++;
- $\text{System.out.flush()}$ in Java;
- $\text{flush(output)}$ in Pascal;
- $\text{stdout.flush()}$ in Python;
- see documentation for other languages.
样例
3 3 1 1 1 0 0 4 5
? 1 1 ? 1 2 ? 1 3 ? 2 1 ? 2 2 ? 2 2 3 3 ? 2 1 3 3 ! 111 000 100
提示
The interaction process in the sample is as follows.
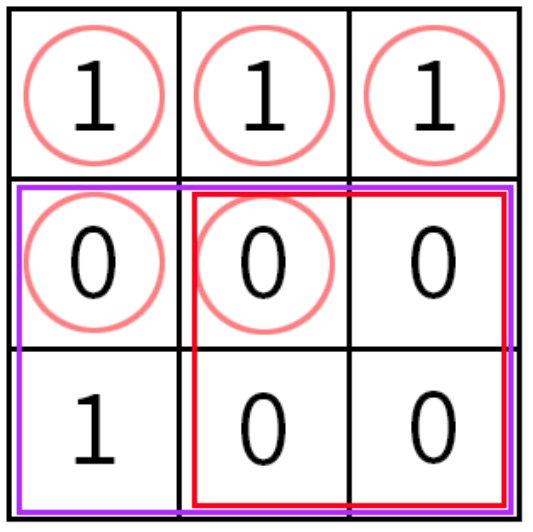
Setsuna first used all the second type of queries to get the numbers in the first five cells.
Then she asked about the $2 \times 2$ submatrix in the lower right corner. JXC told her there are $4$ good pairs, so it is easy to infer that this submatrix is all $0$.
Finally she asked about the $2 \times 3$ submatrix at the bottom. JXC told her there are $5$ good pairs, so it is easy to infer that the lower left corner is $1$.