2020 年 “联想杯”全国高校程序设计在线邀请赛暨第三届上海理工大学程序设计竞赛
K. K-Shift
单点时限: 6.0 sec
内存限制: 256 MB
Setsuna, a lovely girl who likes to play with data structures, is going to share an interesting problem with you which is called $K$-Shift.
An array $A$ can be $K$-Shifted if and only if the length of array $A$ can be divided by $K$ (i.e., $|A|$ must be a multiple of $K$).
When Setsuna $K$-Shift the array $A$, the following events will happen in order:
- From the beginning of $A$, every consecutive $K$ elements are divided into a group, so there will be exactly $\frac{|A|}{K}$ groups.
- In every group, Setsuna does a left circular shift (i.e., the first element in the group will be the last one, and the second element in the group will be the first one, and so on…).
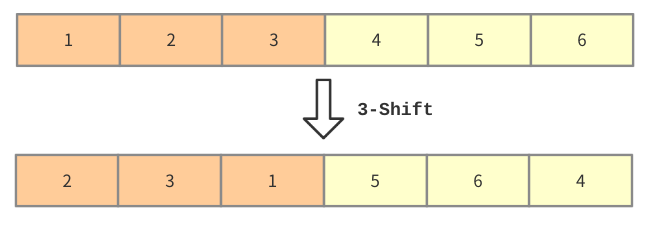
For example, we have $A=\{1,2,3,4,5,6\}$ now. If Setsuna $3$-Shift it , it will become $\{2,3,1,5,6,4\}$.
Now, you have an array $A$ of length $n$ ($1$-indexed). Setsuna will perform two kinds of operations on it:
- Choose an interval $[l,r]$ and an integer $K$, and $K$-Shift the subinterval $\{a_l,a_{l+1},\cdots ,a_r\}$. It is guaranteed that $(r-l+1)$ is a multiple of $K$.
- Choose an interval $[l,r]$ and ask the value of $\sum_{i=l}^r a_i$.
输入格式
The first line contains two integers $n$ and $m$ ($3 \leq n,m \leq 2 \times 10^5$), which indicates the length of the array $A$, and the number of the operations Setsuna will perform.
The second line contains $n$ integers $a_1,a_2,\cdots,a_n (1 \leq a_i \leq 10^9)$.
The $i$-th of the next $m$ lines contains four integers $1,l_i,r_i,K_i (1 \leq l_i \lt r_i \leq n,2\leq K_i \leq 3,K_i|(r_i-l_i+1))$ or three integers $2,l_i,r_i (1 \leq l_i \leq r_i \leq n)$, which respectively represent two different operations.
输出格式
Output the answer to the corresponding operation $2$ in each line.
样例
Input
6 4 1 2 3 4 5 6 1 1 4 2 2 2 3 1 1 6 3 2 2 6
Output
5 20
提示
After the first operation, $\{1,2,3,4,5,6\}$ will become $\{2,1,4,3,5,6\}$.
The sum of elements of indexes in $[2,3]$ is $1+4=5$.
After the third operation, $\{2,1,4,3,5,6\}$ will become $\{1,4,2,5,6,3\}$.
The sum of elements of indexes in $[2,6]$ is $4+2+5+6+3=20$.
通知
比赛状态发生变化，点 OK 刷新。
通知