2020 年 “联想杯”全国高校程序设计在线邀请赛暨第三届上海理工大学程序设计竞赛
M. MITE
单点时限: 8.0 sec
内存限制: 256 MB
Setsuna is playing a computer game called MITE (MogicianCraft Is Too Easy).
In this game, sugar cane is a valuable plant for crafting rockets and trading paper.
Setsuna has a farm. To be a Farm Tycoon, she wants to plant some sugar cane on the land.
The farm can be seen as a two-dimensional plane composed of $n \times m$ blocks, and the size of each block is exactly $1 \times 1$.
There are four types of blocks: sand block, sand block with sugar cane, rock block and water block.
At the beginning, there are only sand blocks and rock blocks. But, Setsuna can replace sand blocks with water blocks, and she can do this any number of times.
To plant sugar cane on a block, Setsuna should follow these rules:
- Sugar cane can only be planted on sand blocks on the farm.
- The sand block sugar cane planted on must be adjacent to at least one water block. Two blocks are considered adjacent if and only if they share an edge.
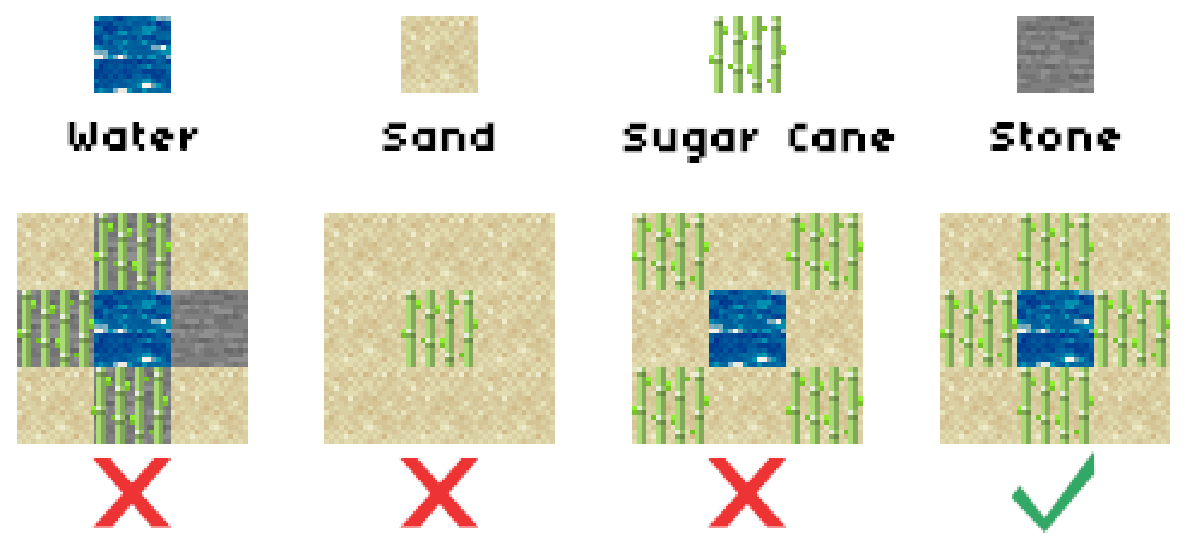
Setsuna wants to know how to maximize the number of blocks that sugar cane can be planted on.
输入格式
The first line of the input contains two integers $n,m(1 \leq n \leq 30,1 \leq m \leq 8)$.
The next $n$ lines contains $m$ characters each, where the $j$-th character of the $i$-th line is $b_{i,j}$ ($b_{i,j}$ is either . if the block $(i,j)$ is a sand block or # if the block $(i,j)$ is a rock block).
输出格式
Print $n$ lines, each of which contains $m$ characters, where the $j$-th character of the $i$-th line is $c_{i,j}$.
$c_{i,j}$ indicates the type of the block $(i,j)$ after reforming.
If the block $(i,j)$ is a water block, $c_{i,j}$ should be O.
If the block $(i,j)$ is a sand block with sugar cane, $c_{i,j}$ should be X.
If the block $(i,j)$ is just a sand block, $c_{i,j}$ should be ..
If the block $(i,j)$ is a rock block, $c_{i,j}$ should be #.
You should make sure the number of X is maximal. If there are multiple solutions, print any.
样例
Input
3 3 ... .#. ...
Output
XOX X#X OXO
Input
3 3 ... #.# ...
Output
XOX #X# XOX
提示
Solutions to sample $1$ and sample $2$ are shown below:
通知
比赛状态发生变化，点 OK 刷新。
通知