EOJ Monthly 2021.10 Sponsored by TuSimple
A. Gold
单点时限: 2.0 sec
内存限制: 512 MB
在平面直角坐标系中，我们称竖直线 $x=-10^{935}$ 和 $x=10^{935}$ 之间的区域为“场地”。
有一个金色飞贼在场地中飞行，规则如下：
- 金色飞贼从场地最左侧（竖直线 $x=-10^{935}$ 上）任意一点出发，到达最右侧（竖直线 $x=10^{935}$ 上）任意一点结束；
- 金色飞贼在水平方向的速度始终为 $1$，而任意时刻竖直方向速度可以为 $-1$ 或 $1$，也就是说，金色飞贼始终朝右上或右下方向飞行，注意金色飞贼可以在任意时刻改变方向，也就是说一条近似于水平直线的运动轨迹也是可能出现的；
- 场地上有 $m$ 个障碍，第 $i$ 个障碍是一条竖直线段，下端点为 $(x_i,y_{i,0})$，上端点为 $(x_i,y_{i,1})$，金色飞贼在飞行过程中不能触碰障碍（包括端点）。
现在请问：金色飞贼在一次完整飞行过程中一定无法经过的区域面积是多少？
输入格式
第一行：一个整数 $m$ ($1\leq m\leq 2\times 10^5$)。
接下来 $m$ 行：其中第 $i$ 行为三个整数 $x_i,y_{i,0},y_{i,1}$ ($0\leq x_i\leq 10^5,\ 0\leq y_{i,0}< y_{i,1}\leq 10^5$)，保证 $y_{i,1}-y_{i,0}$ 为偶数。
输出格式
输出一行：一个实数，表示答案，四舍五入保留两位小数。
样例
Input
2 1 3 5 2 0 4
Output
12.00
Input
2 8 0 8 4 0 8
Output
56.00
提示
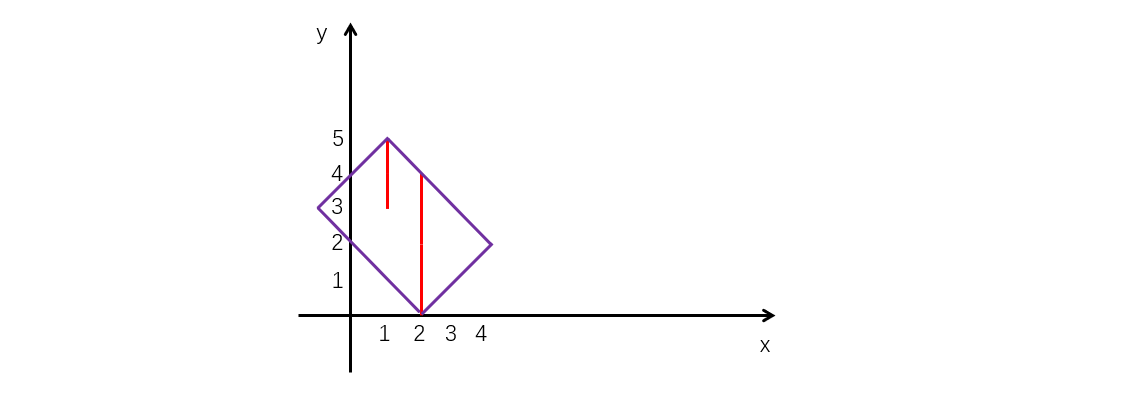
样例 1 解释
如图，红色竖线为两个障碍，紫色矩形为金色飞贼一定无法经过的区域，面积为 $2\sqrt 2\times 3\sqrt 2=12$。
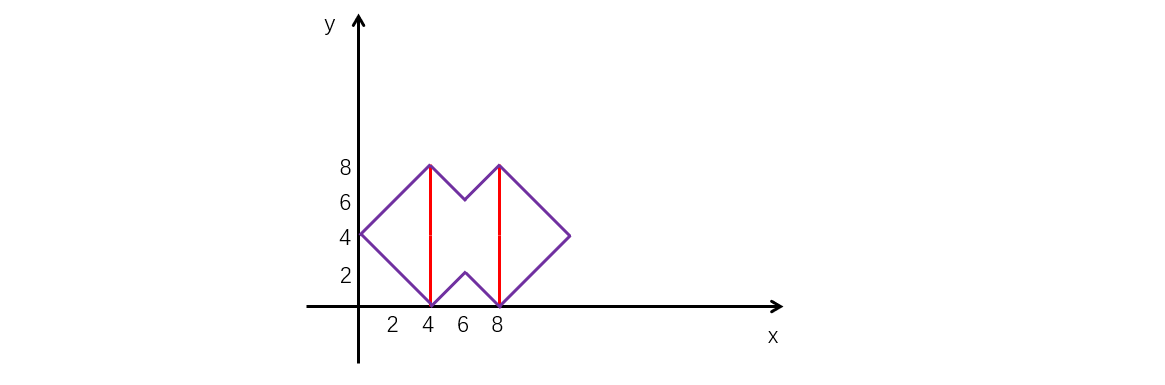
样例 2 解释
如图，红色竖线为两个障碍，紫色区域为金色飞贼一定无法经过的区域，面积为 $56$。
通知
比赛状态发生变化，点 OK 刷新。
通知