96 人解决，131 人已尝试。
113 份提交通过，共有 371 份提交。
3.7 EMB 奖励。
1011. Pseudo-Random Numbers
单点时限: 2.0 sec
内存限制: 256 MB
Computers normally cannot generate really random numbers, but frequently are used to generate sequences of pseudo-random numbers. These are generated by some algorithm, but appear for all practical purposes to be really random. Random numbers are used in many applications, including simulation.
A common pseudo-random number generation technique is called the linear congruential method. If the last pseudo-random number generated was $L$, then the next number is generated by evaluating $( Z \cdot L + I ) \bmod M$, where $Z$ is a constant multiplier, $I$ is a constant increment, and $M$ is a constant modulus. For example, suppose $Z$ is $7$, $I$ is $5$, and $M$ is $12$. If the first random number (usually called the seed) is $4$, then we can determine the next few pseudo-random numbers are follows:
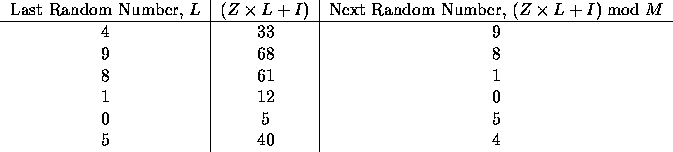
As you can see, the sequence of pseudo-random numbers generated by this technique repeats after six numbers. It should be clear that the longest sequence that can be generated using this technique is limited by the modulus, $M$.
In this problem you will be given sets of values for $Z, I, M$, and the seed, $L$. Each of these will have no more than four digits. For each such set of values you are to determine the length of the cycle of pseudo-random numbers that will be generated. But be careful: the cycle might not begin with the seed!
输入格式
Each input line will contain four integer values, in order, for $Z, I, M, L$. The last line will contain four zeroes, and marks the end of the input data. $L$ will be less than $M$.
输出格式
For each input line, display the case number (they are sequentially numbered, starting with $1$) and the length of the sequence of pseudo-random numbers before the sequence is repeated.
样例
Input
7 5 12 4 5173 3849 3279 1511 9111 5309 6000 1234 1079 2136 9999 1237 2054 4849 7436 3483 0 0 0 0
Output
Case 1: 6 Case 2: 546 Case 3: 500 Case 4: 220 Case 5: 10
题目标签