22 人解决，35 人已尝试。
51 份提交通过，共有 185 份提交。
5.4 EMB 奖励。
1468. Bicriterial routing
单点时限: 6.0 sec
内存限制: 256 MB
The network of pay highways in Byteland is growing up very rapidly. It has become so dense, that the choice of the best route is a real problem. The network of highways consists of bidirectional roads connecting cities. Each such road is characterized by the traveling time and the toll to be paid.
The route is composed of consecutive roads to be traveled. The total time needed to travel the route is equal to the sum of traveling times of the roads constituting the route. The total fee for the route is equal to the sum of tolls for the roads of which the route consists. The faster one can travel the route and the lower the fee, the better the route. Strictly speaking, one route is better than the other if one can travel it faster and does not have to pay more, or vice versa: one can pay less and can travel it not slower than the other one. We will call a route connecting two cities minimal if there is no better route connecting these cities. Unfortunately, not always exists one minimal route – there can be several incomparable routes or there can be no route at all.
Example
The picture below presents an example network of highways. Each road is accompanied by a pair of numbers: the toll and the traveling time.
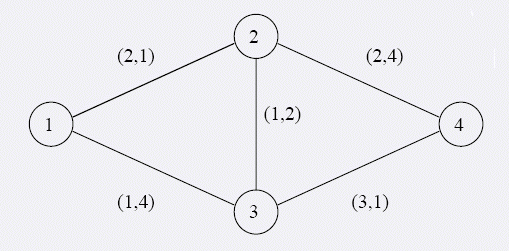
Let us consider four different routes from city 1 to city 4, together with their fees and traveling times: 1-2-4 (fee 4, time 5), 1-3-4 (fee 4, time 5), 1-2-3-4 (fee 6, time 4) and 1-3-2-4 (fee 4, time 10).
Routes 1-3-4 and 1-2-4 are better than 1-3-2-4. There are two minimal pairs fee time: fee 4, time 5 (routes 1-2-4 and 1-3-4) and fee 6, time 4 (route 1-2-3-4). When choosing the route we have to decide whether we prefer to travel faster but we must pay more (route 1-2-3-4), or we would rather travel slower but cheaper (route 1-3-4 or 1-2-4).
Your task is to write a program, which:
Reads the description of the highway network and starting and ending cities of the route.
Computes the number of different minimal routes connecting the starting and ending city, however all the routes characterized by the same fee and traveling time count as just one route; we are interested just in the number of different minimal pairs fee time.
Writes the result.
输入格式
There are four integers, separated by single spaces, in the first line: number of cities $n$ (they are numbered from $1$ to $n$), $1 \le n \le 100$ , number of roads $m$ , $0 \le m \le 300$, starting city $s$ and ending city $e$ of the route, $1 \le s, e \le n$ , $s \neq e$ .
The consecutive $m$ lines describe the roads, one road per line. Each of these lines contains four integers separated by single spaces: two ends of a road $p$ and $r$ , $1 \le p, r \le n$ , $p \neq r$ , the toll $c$ , $0 \le c \le 100$ , and the traveling time $t$ , $0 \le t \le 100$ . Two cities can be connected by more than one road.
输出格式
Your program should write one integer, number of different minimal pairs fee time for routes from $s$ to $e$ , in the first and only line.
样例
Input
4 5 1 4 2 1 2 1 3 4 3 1 2 3 1 2 3 1 1 4 2 4 2 4
Output
2
提示
Hint:
This is the case shown on the picture above.
题目标签