1 人解决，5 人已尝试。
1 份提交通过，共有 32 份提交。
9.9 EMB 奖励。
1784. Cheesy Chess
单点时限: 5.0 sec
内存限制: 256 MB
Chessy Chess is a simple two-person game. It is played on an 8 x 8 board. Each player has one piece. The players take turns in moving their respective pieces.
The first player, say White, has a king. In one move, it can move one position in any of the eight directions, horizontally, vertically or diagonally, as long as it stays on the board. The second player, say Black, has a pawn. In one move, it can move exactly one position downwards. In fact, the pieces have to make such moves. The may not stay at their positions.
The White king is said to capture the Black pawn, if ti moves onto the position currently occuied by the pawn. The aim of the White king is to do exactly this. The aim of the Black pawn is to reach the bottom line of the board safely. As we will see later, however, these are also other ways for White and Black to win.
The game is complicated by the presence of forbidden fields and dangerous fields. A forbidden field is a position where neither the White king , nor the Black pawn may come. A dangerous field is a position where the Black pawn may come, but where the White king may not move onto.
In addition to the fixed dangerous fields, which are dangerous for the entire game, these are (at most) two other, floating dangerous fields, which depend on the position of the Black pawn. The are adjacent to the pawn’s position : the position to the bottom left and bottom right of the pawn, for as for as these positions exit within the boundaries of the board and are not forbidden.
All other positions are called open fields, even if they are occupied by either of the pieces.
For example, we may have the following situation, where forbidden fields, dangerous fields and open fields are denoted by ‘F’, ‘D’ and ‘.’, respectively, the White king is denoted by ‘K’ and the Black pawn is denoted by ‘F’.
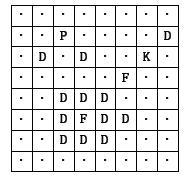
This illustration does not reveal whether the positions occupied by the White and the Black pawn are dangerous or open, and whether the dangrous fields adjacent to the position of the pawn are fixed dangerous fields or not.
Due to a move of the Black pawn, the White king’s position may become dangerous . This is not a problem: in the next move, the White king has to move to another, open field anyway. The White king blocks the Black pawn, if Black is to move, but the position below the pawn is occupied by the White king. In this case, the pawn cannot move.
The game ends, when
-
the White king captures the Black pawn; in this case, White wins;
-
the White king is to move, but cannot move to an open field; in this case, Black wins;
-
the Black pawn is to move, but cannot move to an open field or a dangerous field; if the pawn is at the bottom line of the board, then Black wins, otherwise White wins.
You have to find out which player will win, given that White is the first palyer to move and given that White plays optimally.
输入格式
The first line of input file contains a single number : the number of test cases to follow. Each test case has the following format:
. A description of the board, consisting of 8 lines, corresonding to the 8 lines of the board, from top to bottom. Each line contains a string of 8 characters from {‘F’, ‘D’, ‘.’}. Here ‘F’ denotes a forbidden field, ‘D’ denotes a fixed dangerous field and ‘.’(a period) denotes an open fied.
Of couse, an open field may become dangerous due to the position of the Black pawn.
-
One line with two integers xk and yk (1 <= xk, yk <= 8), separated by a single space, specifying the initial position of the White king. Here, xk denotes the column (counted from left) and yk denotes the row (counted from below).
-
One line with two integers xp and yp (1 <= xp,yp <=8), separated by a single space, specifying the initial position of the Black pawn. Here, xp denotes the column (counted from left) and yk denotes the row (counted from below).
This initial position is not a forbidden field, and is different from the initial position of the White king.
输出格式
Output
For every test case in the input file, the output should contain a single line containing the string “White”(if White wins) or “Black” (if Black wins).
Example
The first test case below corresponds to the pictures in the problem description.
样例
Input
2 ........ .......D ........ .....F. ..DDD... ..DFDD.. ..DDD... ........ 7 6 3 7 ........ ........ ........ ........ ........ ........ ........ ........ 3 1 6 3
Output
Black White Judge Tips Any similarity of this problem to the game Chess is completely coincidental.
题目标签