1 人解决，2 人已尝试。
1 份提交通过，共有 2 份提交。
9.6 EMB 奖励。
2351. Walk
单点时限: 2.0 sec
内存限制: 256 MB
Alice would like to visit Bob. However, they live in a hilly landscape, and Alice doesn’t like to walk in hills. She has a map of the area, showing the height curves. You have to calculate the total altitude climbed, and the total altitude descended, for the route which minimizes these numbers. It does not matter how far she has to walk to achieve this.
Since you don’t know what the landscape looks like in between the height curves, you cannot know exactly how much climb and descent she will actually get in practice, but you should calculate the minimum possible under optimal conditions based on what you can deduce from the map.
The map is represented as an xy grid. Alice lives in (0, 0), and Bob lives in (100 000, 0). The height curves are represented as polygons, where a polygon cannot intersect itself or another polygon. Furthermore, neither Alice nor Bob lives exactly on a height curve.
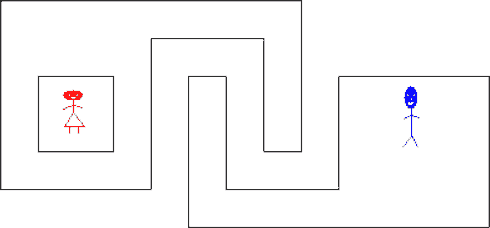
Second test case from sample input (compressed).
输入格式
On the first line one positive number: the number of testcases, at most 100. After that per testcase:
-
One line with 0 ≤ N ≤ 2 500, the number of height curves.
-
One line for each height curve, with 1 ≤ Hi ≤ 1 000 being the height of the curve, 3 ≤ Pi ≤ 2 000 the number of vertices in the polygon, and the vertices x1, y1, …, xPi, yPi having integral values -300 000 ≤ xi, yi ≤ 300 000.
There will be no more than 200 000 polygon vertices in total in all test cases.
输出格式
Per testcase:
- One line with two numbers: the total altitude climbed and the total altitude descended.
样例
Input
2 2 20 3 10 10 0 -10 -10 10 25 3 20 20 0 -20 -20 20 3 100 4 -1 1 1 1 1 -1 -1 -1 300 8 -2 2 2 2 2 -2 5 -2 5 1 6 1 6 -3 -2 -3 50 8 3 3 100001 3 100001 -1 7 -1 7 2 4 2 4 -1 3 -1
Output
5 0 200 250
题目标签