1 人解决,2 人已尝试。
1 份提交通过,共有 2 份提交。
9.6 EMB 奖励。
单点时限: 5.0 sec
内存限制: 256 MB
Isaac B. Manfred always dreamed about being a terribly rich man. When he was a child, he played with banknotes instead of toys. After finishing high school, he quickly became a senior broker in one famous bank. His career rose rapidly and also did his wealth. Unfortunately, the bank crisis changed his life significantly. The broker suddenly became broke.
To gain his money back, I.B.M. spent a lot of time in casinos, trying to earn some money there. Most people who ever tried to get rich in casinos are actually very poor today. But this does not include I.B.M. He is a very clever guy and instead of blindly betting his money, he carefully studies various games and computes the probabilities of losing or winning. First, he tried his luck with Roulette and Blackjack, but found out that the odds of winning a fortune are low.
Recently, I.B.M. started to study dice games. He found several of them similar to a trademarked game called Yahtzee! The rules sometimes vary but basic principles are the same. To give you an idea, we will describe a simplified version of such rules.
The game consists of rounds. In each round, a player rolls five dice. After the first roll, it is possible to keep some of the dice and re-roll the rest of them. Any number of dice can be rerolled (including none or all of them). If the re-rolled dice still do not fit the player’s intentions, it is possible to re-roll some of them again, for the third and final time. After at most two such re-rolls, the player must assign the result to one of possible combinations and the round is scored according to that combination.
The following table shows the list of combinations, conditions that must be satisfied to use them, and the number of points scored when the combination is used.
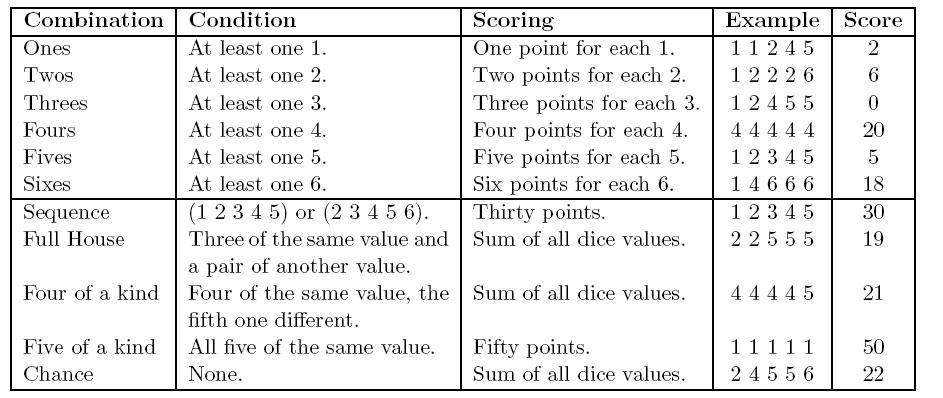
A small example: The player rolls 2, 3, 6, 6, 5. The two 6’s are kept and the three remaining dice re-rolled, they give new values: 1, 1, 6. The player may now choose to score 20 points immediately for a Full House. Instead, he or she decides to re-roll the two 1’s again, in hope there will be another 6. The dice give 4 and 5 and the player will score either 18 points for Sixes or 27 points for Chance.
The main point of the game is that there are eleven combinations and eleven rounds. During the whole game, each combination must be used exactly once. It may happen that some result would not fit into any available combination. In such a case, the player must select some combination anyway, scoring zero points for that round and losing the possibility to use that combination later. These rules make the game very tricky, especially at the end, when the combinations have been almost exhausted.
Now, we get back to Isaac. He found a casino with an electronic version of this dice game. After carefully watching many games of other players, he was able to crack the random-number generator used in the machine. Therefore, he is able to predict the following rolls exactly. What an opportunity! However, it is still not easy to find the optimal strategy. If you write a program that would help him to become rich, he may share some of his money with you.
The input contains several scenarios, each of them specified on a single line. The line contains three numbers separated by a space: A, C, and X0. These numbers describe the random-number generator: A is called a multiplier (1 ≤ A ≤ 231), C is an increment (0 ≤ C ≤ 231), and X0 is the initial seed (0 ≤ X0 ≤ 231). The last scenario is followed by a line containing three zeros. The generator is a linear congruential generator, which means that the next random number is calculated from the previous one using the following formula:
Xn+1 = (A * Xn + C) mod 232
The modulo operation specifies that only the lowest 32 bits of the result are used, the rest is discarded. Numbers X1, X2, X3 … constitute a pseudo-random sequence, each of them determines the result of one individual roll of a dice. With congruential generators, the “randomness” of the numbers is in their higher bits only ― therefore, to get a result of the n-th roll (starting with n = 1), we discard lower 16 bits of the number Xn and compute the remainder when the number in bits 16-31 is divided by six. This gives a number between 0 and 5, by adding one, we get a number shown on a dice:
roll(n) = [floor(Xn/216) mod 6]+1
For example, when A = 69069, C = 5, and the X0 = 0 is zero, we get the following sequence of
“random” rolls: 1, 6, 6, 3, 2, 4, 3, 2, 3, 5, 1, 6, 6, 4, 5, 1, 3, 4, 1, …
For each scenario, print one integer number: the maximal number of points that may be scored in a game determined by the given generator. The score is calculated after 11 rounds as the sum of scores in all combinations.
69069 5 0 69069 5 2 1664525 1013904223 177 1103515245 12345 67890 0 0 0
235 194 241 235
1 人解决,2 人已尝试。
1 份提交通过,共有 2 份提交。
9.6 EMB 奖励。