0 人解决，1 人已尝试。
0 份提交通过，共有 4 份提交。
9.9 EMB 奖励。
2671. Alice and Bob
单点时限: 5.0 sec
内存限制: 256 MB
Alice and Bob are in love with each other, but they have difficulty going out on a date ― Alice is a very busy graduate student at the ACM university.
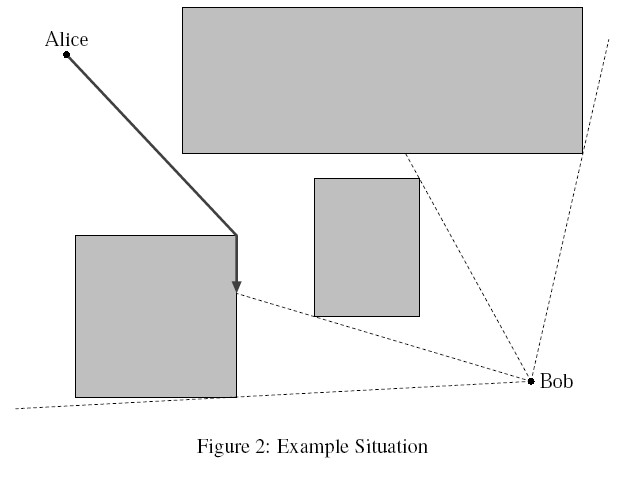
For this reason, Bob came to the ACM university to meet her on a day. He tried to reach the meeting spot but got lost because the campus of the university was very large. Alice talked with him via mobile phones and identified his current location exactly. So she told him to stay there and decided to go to the place where she would be visible to him without interruption by buildings.
The campus can be considered as a two-dimensional plane and all buildings as rectangles whose edges are parallel to $x$-axis or $y$-axis. Alice and Bob can be considered as points. Alice is visible to Bob if the line segment connecting them does not intersect the interior of any building. Note that she is still visible even if the line segment touches the borders of buildings.
Since Alice does not like to walk, she wants to minimize her walking distance. Can you write a program that finds the best route for her?
输入格式
The input contains multiple datasets. The end of the input is indicated by a line containing a single zero.
Each dataset is formatted as follows.
$N \
x_{11} \ y_{11} \ x_{12} \ y_{12} \
x_{21} \ y_{21} \ x_{22} \ y_{22} \
\vdots \
x_{N1} \ y_{N1} \ x_{N2} \ y_{N2} \
A_x \ A_y \ B_ x \ B_y$
$N$ ($0 < N \le 30$) is the number of buildings. The $i$-th building is given by its bottom left corner $(x_{i1}, y_{i1})$ and up right corner $(x_{i2}, y_{i2})$. $(A_x, A_y)$ is the location of Alice and $(B_x, B_y)$ is that of Bob. All integers $x_{i1}, y_{i1}, x_{i2}, y_{i2}, A_x, A_y, B_x$ and $B_y$ are between $-1000$ and $1000$, inclusive. You may assume that no building touches or overlaps other buildings.
输出格式
For each dataset, output a separate line containing the minimum distance Alice has to walk.
The value may contain an error less than or equal to $10^{-4}$. You may print any number of digits after the decimal point.
样例
Input
1 3 3 7 7 2 2 8 2 2 2 5 5 9 6 1 9 5 1 5 10 5 2 2 1 3 2 2 3 3 4 1 1 4 4 1 3 3 7 7 1 5 9 5 1 3 3 7 7 1 5 8 5 1 3 3 7 7 1 5 10 5 0
Output
0.000 0.000 0.000 5.657 6.406 4.992