2 人解决，7 人已尝试。
2 份提交通过，共有 13 份提交。
9.5 EMB 奖励。
2712. Aerodynamics
单点时限: 5.0 sec
内存限制: 256 MB
Bill is working in a secret laboratory. He is developing missiles for national security projects. Bill is the head of the aerodynamics department.
One surprising fact of aerodynamics is called Whitcomb area rule. An object flying at high-subsonic speeds develops local supersonic airows and the resulting shock waves create the effect called wave drag.Wave drag does not depend on the exact form of the object, but rather on its cross-sectional profile.
Consider a coordinate system with $OZ$ axis pointing in the direction of object’s motion. Denote the area of a section of the object by a plane z = $z_{0}$ as $S(z_{0})$. Cross-sectional profile of the object is a function $S$ that maps $z_{0}$ to $S(z_{0})$. There is a perfect aerodynamic shape called Sears-Haack body. The closer cross-sectional profile of an object to the cross-sectional profile of Sears-Haack body, the less wave drag it introduces. That is an essence of Whitcomb area rule.
Bill’s department makes a lot of computer simulations to study missile’s aerodynamic properties before it is even built. To approximate missile’s cross-sectional profile one takes samples of $S(z_{0})$ for integer arguments $z_{0}$ from $z_{min}$ to $z_{max}$.
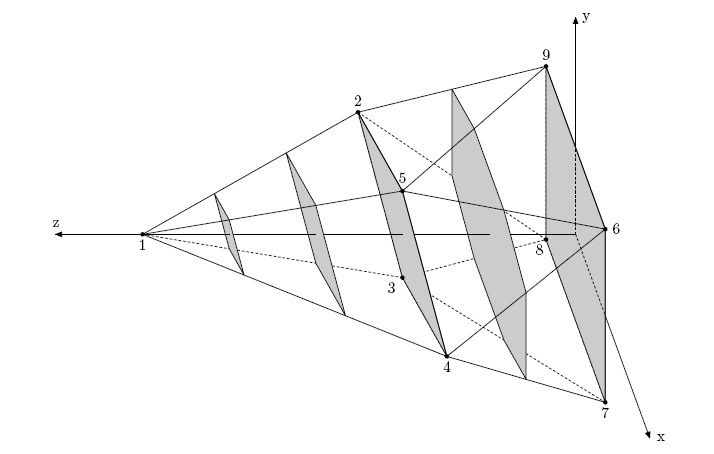
Your task is to find the area $S(z_{0})$ for each integer $z_{0}$ from $z_{min}$ to $z_{max}$, inclusive, given the description of the missile. The description of the missile is given to you as a set of points. The missile is the minimal convex solid containing all the given points. It is guaranteed that there are four points that do not belong to the same plane.
输入格式
The first line of the input file contains three integer numbers: $n$, $z_{min}$ and $z_{max}$ ($4 \le n \le 100,0 \le z_{min} \le z_{max} \le 100$). The following $n$ lines contain three integer numbers each: $x$, $y$, and $z$ coordinates of the given points. All coordinates do not exceed $100$ by their absolute values. No two points coincide. There are four points that do not belong to the same plane.
输出格式
For each integer $z_{0}$ from $z_{min}$ to $z_{max}$, inclusive, output one floating point number: the area $S(z_{0})$. The area must be precise to at least 5 digits after decimal point.
样例
Input
9 0 5 0 0 5 -3 0 2 0 -1 2 3 0 2 0 1 2 2 2 0 2 -2 0 -2 -2 0 -2 2 0
Output
16.00000 14.92000 10.08000 4.48000 1.12000 0.00000
题目标签