0 人解决,1 人已尝试。
0 份提交通过,共有 2 份提交。
9.9 EMB 奖励。
单点时限: 10.0 sec
内存限制: 256 MB
There is this big museum, full of fancy rooms and shiny corridors. It is so large that planning any tour in it becomes a serious issue. This is where your help is necessary. You are to help in planning signs that will make navigation through the whole building much easier. The idea is that if a room has d doors leading through corridors to other rooms, these doors and corresponding corridors are (locally) labeled with numbers 1, 2, . . . , d. Then all visitors are advised to follow a simple procedure. If they are in room v at the very beginning of their tour, they should choose door labelled with 1 and pass through
the corresponding corridor If they are in room v and they entered it through door labelled with i, they should pick the door labelled with the next number (i.e. i + 1 if i < d and 1 if i = d) and pass through corresponding corridor. Here is a simple example, in which tourists start in room 1 and visit rooms 1, 2, 3, 4, 5, 6 in this order passing through each corridor at least once:
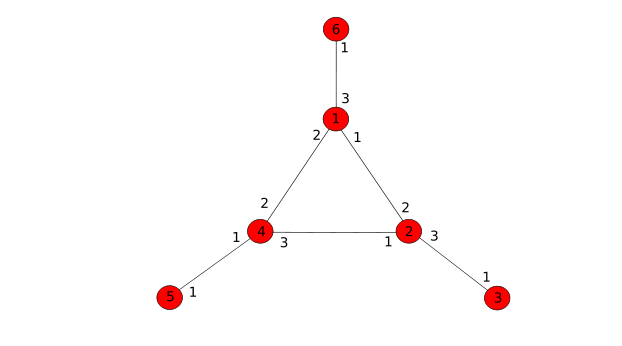
Exhibits in this museum are not only in rooms but also in corridors connecting different rooms. After all, the corridors are well suited for displaying paintings and photography! Thus we want to ensure that the tourists that follow the rules will pass through each corridor at least once, assuming they do not get bored easily and walk long enough, irrespectively of the room they started the tour in. Your task is to find such a labelling.
It turns out that there are at most 3 corridors outgoing from each room and the whole museum is connected, i.e. it is possible to walk between any two rooms, possibly passing through other rooms along the way. All corridors outgoing from a single room lead to different rooms.
The input contains several test cases. The first line contains the number of test cases t (t ≤ 100). Each test begins with a line containing the number of rooms n (3 ≤ n ≤ 105 ). The next n lines contain description of all corridors. i-th of them described corridors connecting the i-th room with others. It begins with an integer d (1 ≤ d ≤ 3), the number of doors in this room. d integers r1 , r2 , . . . , rd follow, giving numbers of rooms that those doors lead to (1 ≤ rj ≤ n and rj = rk if j = k and rj = i). All corridors are bidirectional, so if there is door from room x to room y, there is door from room y to room x as well. Total size of the input will not exceed 50MB.
For each test case output exactly n lines. i-th of them should contain numbers of rooms directly connected by corridors with room i, in order of their assigned labels. You may assume that a valid labelling of doors always exists, you just need to find one.
2 6 3 4 2 3 3 5 1 3 3 6 1 2 1 1 1 2 1 3 4 2 2 4 2 1 3 2 2 4 2 1 3
3 4 2 3 3 5 3 1 3 6 1 2 1 1 1 2 1 3 2 2 4 2 1 3 2 2 4 2 1 3
0 人解决,1 人已尝试。
0 份提交通过,共有 2 份提交。
9.9 EMB 奖励。