2 人解决，11 人已尝试。
2 份提交通过，共有 77 份提交。
9.8 EMB 奖励。
5564. Roll the dice
单点时限: 2.0 sec
内存限制: 512 MB
有一个 $n \times m$ 的矩阵，该矩阵的行和列以整数编号，行从上往下按照 $1$ 到 $n$ 依次编号，列从左往右按照 $1$ 到 $m$ 依次编号，单元格 $(i, j)$ 是第 $i$ 行与第 $j$ 列相交的单元格 $(1 \leqslant i \leqslant n, \ 1 \leqslant j \leqslant m)$。
在这个矩阵上有一个骰子$^{[1]}$，骰子初始时位于单元格 $(sx, sy)$，且 $1$ 朝上，$\texttt{5}$ 朝左。有如下四种操作：
- 让骰子向右滚动一格，同时骰子向右旋转 $90^{\circ}$；
即如果骰子操作前位于 $(i, j)$，且 $\texttt{1}$ 朝上，$\texttt{5}$ 朝左，则操作后位于 $(i, j + 1)$，且 $\texttt{5}$ 朝上，$\texttt{6}$ 朝左。
$\ \ $ - 让骰子向左滚动一格，同时骰子向左旋转 $90^{\circ}$；
即如果骰子操作前位于 $(i, j)$，且 $\texttt{1}$ 朝上，$\texttt{5}$ 朝左，则操作后位于 $(i, j - 1)$，且 $\texttt{2}$ 朝上，$\texttt{1}$ 朝左。
$\ \ $ - 让骰子向前滚动一格，同时骰子向前旋转 $90^{\circ}$；
即如果骰子操作前位于 $(i, j)$，且 $\texttt{1}$ 朝上，$\texttt{5}$ 朝左，则操作后位于 $(i + 1, j)$，且 $\texttt{4}$ 朝上，$\texttt{5}$ 朝左。
$\ \ $ - 让骰子向后滚动一格，同时骰子向后旋转 $90^{\circ}$；
即如果骰子操作前位于 $(i, j)$，且 $\texttt{1}$ 朝上，$\texttt{5}$ 朝左，则操作后位于 $(i - 1, j)$，且 $\texttt{3}$ 朝上，$\texttt{5}$ 朝左。
注意操作后骰子的位置不能超出矩阵的边界，即必须保证骰子的位置 $(i, j)$ 始终满足 $1 \leqslant i \leqslant n, \ 1 \leqslant j \leqslant m$。
请问最少需要进行多少次操作才能使得骰子到达 $(tx, ty)$，且 $\texttt{1}$ 仍朝上（如果到达了 $(tx, ty)$，但 $\texttt{1}$ 不朝上，则仍需要继续进行操作），如果始终无法在满足条件的情况下到达 $(tx, ty)$，则输出 $-1$。
[1]: 骰子是一种立体小方块，六面分别刻 $\texttt{1}, \ \texttt{2}, \ \texttt{3}, \ \texttt{4}, \ \texttt{5}, \ \texttt{6}$，其中 $\texttt{1}$ 和 $\texttt{6}$ 相对，$\texttt{2}$ 和 $\texttt{5}$ 相对，$\texttt{3}$ 和 $\texttt{4}$ 相对，具体空间形态如图：
输入格式
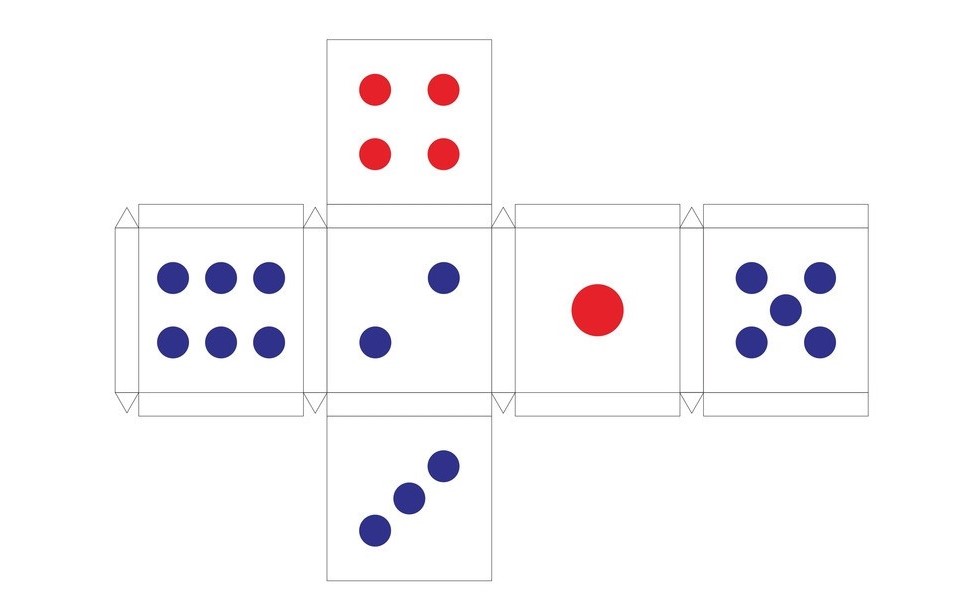
每个测试点由多个测试用例组成。
输入的第一行包含一个整数 $t \ (2 \leqslant t \leqslant 2 \times 10^5)$，表示测试用例的数量。然后是每个测试用例的说明。
每个测试用例的第一行也是唯一一行包含 $6$ 个整数： $n, \ m, \ sx, \ sy, \ tx, \ ty \ (1 \leqslant n, m \leqslant 10^{18}, \ 1 \leqslant sx, tx \leqslant n, \ 1 \leqslant sy, ty \leqslant m)$，含义见题面描述。
输出格式
对于每个测试用例，输出一个整数，如果始终无法在满足条件的情况下到达 $(tx, ty)$，输出 $-1$，否则输出最小操作次数。
样例
Input
4 1 2 1 1 1 2 5 5 1 1 5 5 5 5 3 3 5 5 3 4 1 1 3 4
Output
-1 8 4 5
创建: 8 月，2 周前.
修改: 7 月，3 周前.
最后提交: 3 月，1 周前.
来源: N/A
题目标签