Difference between revisions of "2019 Multi-University,HDU Day 2"
Xiejiadong (talk | contribs) |
Xiejiadong (talk | contribs) |
||
| Line 33: | Line 33: | ||
Upsolved Xiejiadong. | Upsolved Xiejiadong. | ||
| − | 题意:给出 $n$ 个点,要将 $n$ 个点分到两个集合。给出 $m$ 对关系,如果关系中的两个点都位于 $ | + | 题意:给出 $n$ 个点,要将 $n$ 个点分到两个集合。给出 $m$ 对关系,如果关系中的两个点都位于 $1$ 集合,价值 $A$ ;都位于 $2$ 集合,价值 $C$ ;位于两个集合,价值 $B$ 。 |
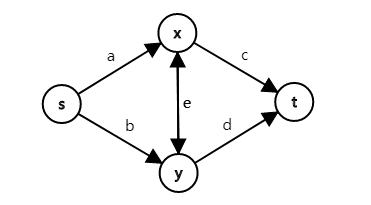
题解:用最小割建图,利用如图的网络,考虑一对关系 $u,v$ : | 题解:用最小割建图,利用如图的网络,考虑一对关系 $u,v$ : | ||
[[File:1008.png]] | [[File:1008.png]] | ||
| + | |||
| + | * 对于都位于 $1$ 集合,价值 $A$ ,我们可以割掉边 $a,b$ ,即 $a+b=C+B$ ; | ||
| + | |||
| + | * 对于都位于 $2$ 集合,价值 $C$ ,我们可以割掉边 $c,d$ ,即 $c+d=A+B$ ; | ||
| + | |||
| + | * 对于位于不同集合,价值 $B$ ,我们可以割掉边 $c,d$ ,即 $a+e+d=b+e+c=C+A$ ; | ||
| + | |||
| + | 所以我们可以有 $a=b=\frac{C+B}{2},c=d=\frac{A+B}{2},e=B-\frac{A}{2}-\frac{C}{2}$ 。 | ||
| + | |||
| + | 显然题目给出 $B=\frac{A}{4}+\frac{C}{3}$ ,就是为了防止出现负边权的边。 | ||
== Problem I == | == Problem I == | ||
Revision as of 15:49, 24 July 2019
Problem A
Unsolved.
Problem B
Upsolved by Kilo_5723 && Weaver_zhu. (-1)
没写完。赛后 2min 补题。
Problem C
Unsolved.
Problem D
Unsolved.
Problem E
Solved by Weaver_zhu && Kilo_5723. 01:40:33 (+)
Problem F
Unsolved.
Problem G
Unsolved.
Problem H
Upsolved Xiejiadong.
题意:给出 $n$ 个点,要将 $n$ 个点分到两个集合。给出 $m$ 对关系,如果关系中的两个点都位于 $1$ 集合,价值 $A$ ;都位于 $2$ 集合,价值 $C$ ;位于两个集合,价值 $B$ 。
题解:用最小割建图,利用如图的网络,考虑一对关系 $u,v$ :
- 对于都位于 $1$ 集合,价值 $A$ ,我们可以割掉边 $a,b$ ,即 $a+b=C+B$ ;
- 对于都位于 $2$ 集合,价值 $C$ ,我们可以割掉边 $c,d$ ,即 $c+d=A+B$ ;
- 对于位于不同集合,价值 $B$ ,我们可以割掉边 $c,d$ ,即 $a+e+d=b+e+c=C+A$ ;
所以我们可以有 $a=b=\frac{C+B}{2},c=d=\frac{A+B}{2},e=B-\frac{A}{2}-\frac{C}{2}$ 。
显然题目给出 $B=\frac{A}{4}+\frac{C}{3}$ ,就是为了防止出现负边权的边。
Problem I
Solved by Xiejiadong. 03:50:48 (+1)
题意:对于所有 $k$ ,求所有长度为 $k$ 的回文串个数,且回文串满足前一半也是回文串。
题解:根据自动机的同性,发明了一遍回文树。
回文自动机上的 fail 指针的性质就是,如果 $x$ 是 $y$ 的父亲,那么 $x$ 是 $y$ 的后缀。而 $x$ 和 $y$ 都满足是回文串,所以只要 $y$ 的祖先中存在长度为 $(|y|+1)/2$ 的,就满足了题目要求的回文串。
于是对于所有满足这样性质的结点 $y$ 计数即可。
Problem J
Solved by Kilo_5723. 00:22:49 (+1)
Problem K
Solved by Xiejiadong && Kilo_5723. 01:09:19 (+1)
题意:每次询问一个区间能组成的周长最长的三角形周长。
题解:如果我们确定了一个区间里的某一条边为最长边,那么显然组成的三角形的另两条边一定是长度比它小但是最接近的两条边。
也就是说,组成三角形的三条边一定是区间里长度排序以后连续的三条边。
考虑无法组成三角形的情况,一定存在 $a>b+c$ ,也就是说,如果不成立的话,长度可以至少减少一半,于是就可以直接暴力了。
不断的询问最大的长度,次大的长度,直到询问到三角形或者无解。
区间 $k$ 大值,用主席树维护就好了。
Problem L
Solved by Kilo_5723 && Xiejiadong. 03:06:54 (+)