Difference between revisions of "2019 Multi-University,HDU Day 2"
Xiejiadong (talk | contribs) |
Xiejiadong (talk | contribs) |
||
| Line 81: | Line 81: | ||
Solved by Kilo_5723. 00:22:49 (+1) | Solved by Kilo_5723. 00:22:49 (+1) | ||
| − | 题意:有一个 $0$ ~ $2^{n}-1$ 的数 $x$,可以一次性询问多个 $x & k$ 是否等于 $k$,求不同询问方案的总数。 | + | 题意:有一个 $0$ ~ $2^{n}-1$ 的数 $x$,可以一次性询问多个 $x \& k$ 是否等于 $k$,求不同询问方案的总数。 |
题解:要确定 $2^n$ 种不同的可能性,至少需要询问 $n$ 次,因此最好的询问就是询问所有的 $2^{i}(0 \le i < n)$。方案总数即为 $n!$。 | 题解:要确定 $2^n$ 种不同的可能性,至少需要询问 $n$ 次,因此最好的询问就是询问所有的 $2^{i}(0 \le i < n)$。方案总数即为 $n!$。 | ||
Revision as of 08:40, 28 July 2019
Problem A
Unsolved.
Problem B
Upsolved by Kilo_5723 && Weaver_zhu. (-1)
没写完。赛后 2min 补题。
题意:求字典序最大和最小的最长合唱队型。
题解:先反向做一遍合唱队形。将一个位置拆成两个点。$(i,1)$ 的权值是从第 $i$ 个节点开始的最长合唱队型的长度,$(i,2)$ 的权值是从第 $i$ 个节点开始的最长下降子序列的长度。
我们将节点按照权值分类。由于每一个第 $k$ 层点的权值都是从 $k-1$ 层中的某一个点推导的,所以可以保证从顶层任何一个点出发,一定能找到一条通往底层的路径。因此,$O(n)$ 遍历两次,每次找出下一层和当前层连通的字典序最大/最小的点,连起来就是字典序最大和最小的合唱队形。
Problem C
Unsolved.
Problem D
Unsolved.
Problem E
Solved by Weaver_zhu && Kilo_5723. 01:40:33 (+)
题意:随机生成一个 $1$ ~ $n$ 的排列,每次将排列的逆序对数量加入答案,再取出序列的一个子序列,直到序列为空。求答案的期望。
题解:问题可以拆成两部分。
1)每个长度为 $m$ 的序列对答案贡献的期望值是 $\frac{m \cdot (m+1)}{4}$。
2)令 $f(n)$ 是长度为 $n$ 的序列在以后的所有过程中对答案贡献的期望值,则 $f(n)=\sum_{i=0}^{n} C(n,i) \cdot f(i)$。移项后就能求出每一个 $f(n)$ 的值。
对输入为 $n$,答案 $ans=\frac{\sum_{i=1}^{n}f(i)}{n}$。
Problem F
Unsolved.
Problem G
Unsolved.
Problem H
Upsolved Xiejiadong.
题意:给出 $n$ 个点,要将 $n$ 个点分到两个集合。给出 $m$ 对关系,如果关系中的两个点都位于 $1$ 集合,价值 $A$ ;都位于 $2$ 集合,价值 $C$ ;位于两个集合,价值 $B$ 。
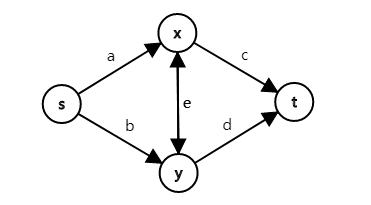
题解:用最小割建图,利用如图的网络,考虑一对关系 $u,v$ :
- 对于都位于 $1$ 集合,价值 $A$ ,我们可以割掉边 $a,b$ ,即 $a+b=C+B$ ;
- 对于都位于 $2$ 集合,价值 $C$ ,我们可以割掉边 $c,d$ ,即 $c+d=A+B$ ;
- 对于位于不同集合,价值 $B$ ,我们可以割掉边 $a,e,d$ 或者边 $b,e,c$ ,即 $a+e+d=b+e+c=C+A$ ;
所以我们可以有 $a=b=\frac{C+B}{2},c=d=\frac{A+B}{2},e=\frac{A}{2}+\frac{C}{2}-B$ 。
显然题目给出 $B=\frac{A}{4}+\frac{C}{3}$ ,就是为了防止出现负边权的边。
Problem I
Solved by Xiejiadong. 03:50:48 (+1)
题意:对于所有 $k$ ,求所有长度为 $k$ 的回文串个数,且回文串满足前一半也是回文串。
题解:根据自动机的同性,发明了一遍回文树。
回文自动机上的 fail 指针的性质就是,如果 $x$ 是 $y$ 的父亲,那么 $x$ 是 $y$ 的后缀。而 $x$ 和 $y$ 都满足是回文串,所以只要 $y$ 的祖先中存在长度为 $(|y|+1)/2$ 的,就满足了题目要求的回文串。
于是对于所有满足这样性质的结点 $y$ 计数即可。
Problem J
Solved by Kilo_5723. 00:22:49 (+1)
题意:有一个 $0$ ~ $2^{n}-1$ 的数 $x$,可以一次性询问多个 $x \& k$ 是否等于 $k$,求不同询问方案的总数。
题解:要确定 $2^n$ 种不同的可能性,至少需要询问 $n$ 次,因此最好的询问就是询问所有的 $2^{i}(0 \le i < n)$。方案总数即为 $n!$。
Problem K
Solved by Xiejiadong && Kilo_5723. 01:09:19 (+1)
题意:每次询问一个区间能组成的周长最长的三角形周长。
题解:如果我们确定了一个区间里的某一条边为最长边,那么显然组成的三角形的另两条边一定是长度比它小但是最接近的两条边。
也就是说,组成三角形的三条边一定是区间里长度排序以后连续的三条边。
考虑无法组成三角形的情况,一定存在 $a>b+c$ ,也就是说,如果不成立的话,长度可以至少减少一半,于是就可以直接暴力了。
不断的询问最大的长度,次大的长度,直到询问到三角形或者无解。
区间 $k$ 大值,用主席树维护就好了。
Problem L
Solved by Kilo_5723 && Xiejiadong. 03:06:54 (+)