2018 ECNU One,Two,Three,AK's ICPC/CCPC Training Contest

2018 ECNU One,Two,Three,AK's ICPC/CCPC Training Contest

Prepared by One,Two,Three,AK

由于是互鏼，没有用整套题目，重组了一部分我们训练中遇到的好题，所以大部分题目的难度集中在mid-/+。可能比赛不会有区分度，但都是值得尝试与思考的题目，赛后把这些题目都补了，一定会有收获！

Problem A

算法：Trie树

难度：mid+

题意：可以将两个字符串首位相接，或者取单个字符串，求本质不同的字符串有几个。

题解：用Trie树来跑，按照前缀和后缀分别构建Trie树，显然这样做是会重复的。

而重复的一段必然是由于中间段相同所引起的。那么我们可以处理前缀的后缀和后缀的前缀相同的个数，用类似于二元容斥的方法来判重。

Problem D

算法：最短路

难度：mid-

题意：给出一条链，求链上边的子集，使得起点到终点了联通。

题解：绝对的自闭题。

对于每一个点的不同次访问，把每个点拆开了，对于访问次数不同但是一样的点，两两连边权为0的边，然后从起点到终点跑最短路就行了。

Problem E

算法：dp

难度：mid-

题意：给出一个数的数字和以及数字的平方和，求最小满足题意的数。

题解：内存卡的很紧。

用$f[I][j]$表示$s1$位$i$和$s2$为$j$的最小值

显然位数位$100$是存不下的，我们就存当前位置，然后递归一下，把每一位的答案拿出来，排个序，从小到大输出即可。

Problem G

算法：构造，dfs

难度：mid

题意：把$1-n$这$n$个数，分成$m$堆，使得$m$堆数的和相等。

题解：首先考虑没有解的情况。

显然，没有解的无非是$n$无法整除$m$，或者是$\frac{n}{m}<n$（即最大的一个数无法放入任何一组）

将较大的数，每$2\times m$为一组，放入$m$堆中，从小到大相应配对，显然和相等

当剩下的数不足$3\times m$个时，直接暴力dfs配对即可。

Problem J

算法：二分答案

难度：easy+

题意：给每个人分配一个相同的长度，使得每个人可以在自己的区间里面找出互不重叠的区间。

题解：用 long double 来二分答案，然后暴力枚举分母，找出分数的表示。

Problem K

算法：构造

难度：mid

题意：从0出发，用$a$次$\pm 1$,$b$次$\pm 2$,$c$次$\pm 3$遍历所有的$0$到$a+b+c$点。

题解：先把$c$次$\pm 3$的处理掉。我们通过向右、向左、再向右三部分，把前面的一部分填满，并且最后填的一个的左边已经全部填满，右边全部没有填过

再向右一步一步填，剩下一个$\pm 1$用来在最后改变方向，剩下的$\pm 2$我们用过向右、转弯、向左来填满右边剩下的部分

注意各类情况的处理与细节问题

Problem M

算法：二分答案+思想

难度：mid+

题意：每层每个格子里的数为其下方三个数的中位数，给出底层的数，求顶层的数。

题解：考虑二分答案，假设当前需要验证的答案为$x$，表示答案$≥x$是否成立

那么，根据最下面一行和$≥x$的关系，我们可以得到底层的$0/1$数列，$1$表示$≥x$

我们现在得到了底层的$0/1$数列，而题目所给的条件，上一层的一格为$1$，当且仅当下一层与之对应的三个中至少有两个$1$

现在，符合情况的话，那么就是顶层为$1$

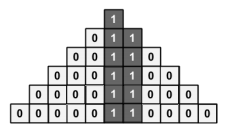
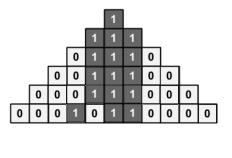
我们可以画画图来分析一下底层的情况，如何向上传导

我们可以发现，当出现连续的两个$1$的时候，他们所对应的的上面，全部为$1$

那么，这样的情况如何向外拓展呢？

我们发现，当连续的两个$1$旁边出现隔着一个位置的$1$的是否，这个全是$1$的竖行，可以向着隔着一个位置的$1$的方向拓展一列

那么我们只需要正着反着，各扫一遍

这样一来，我们就可以在$O(2n)$的时间内验证答案了

还有一种比较特殊的情况是，底层不需要出现连续的两个$1$

特判一下

总的时间复杂度是$O(3n*logn)$