2018 Multi-University, Nowcoder Day 4

Problem A

Solved by zerol. 02:17 (+2)

Problem C

Solved by ultmaster. 02:57 (+1)

题意：[math]\displaystyle{ a_n = \begin{cases} 0 & n = 1, \\ a_{\lfloor \frac{n}{2} \rfloor } + (-1)^{n(n+1)/2} & n \ge 2 \end{cases} }[/math]，求 $\sum_{i=1}^n |a_i|$。

题解：$a_n$ 只跟其二进制上每相邻两位组成的数（0 或 1 或 2 或 3）有关。所以数位 DP 即可。数组开小了改了半天。。。。

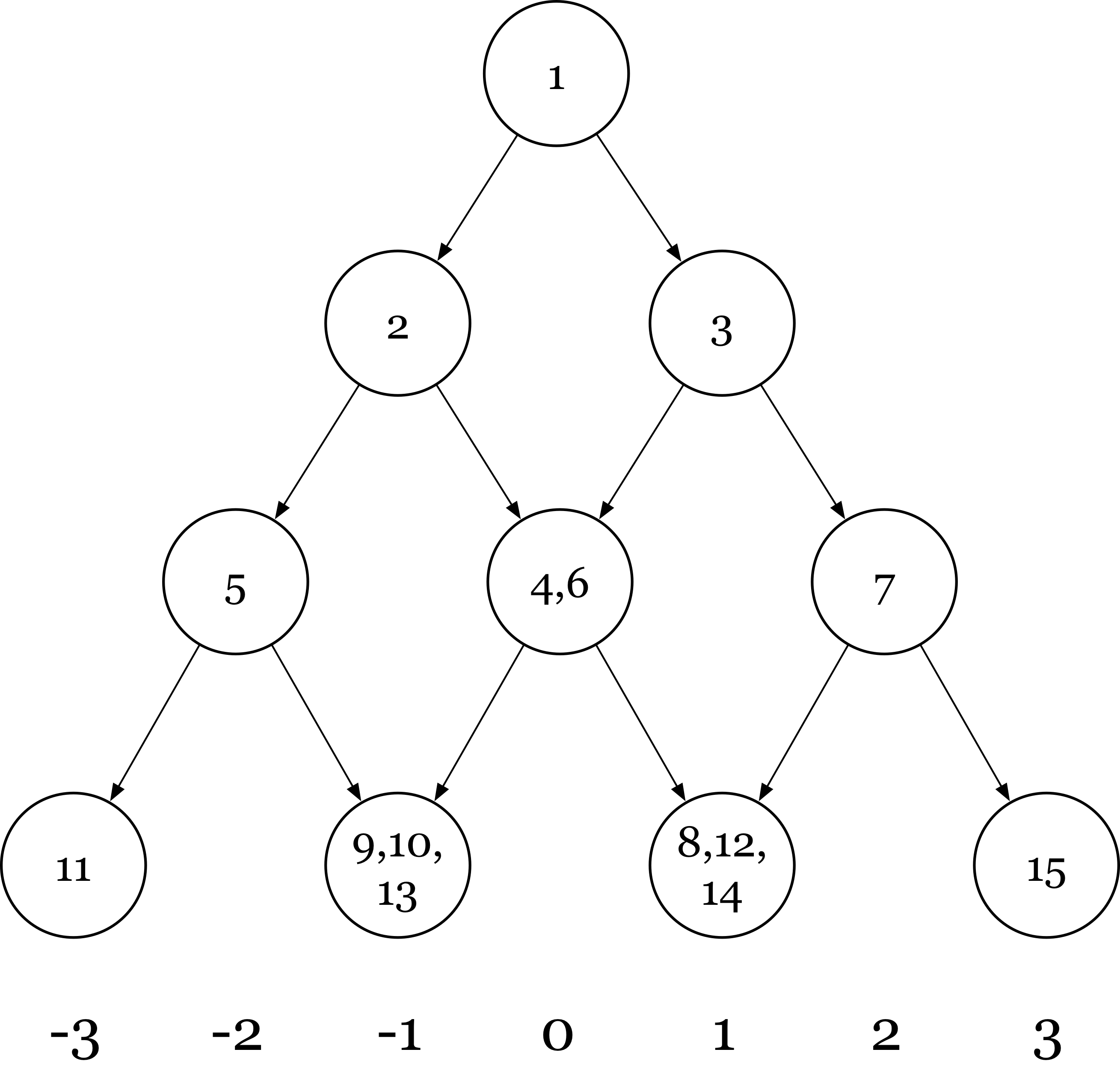
另解 (by oxx): 发现写在一个二叉树里以后，数目刚好成一个杨辉三角。然后随便算算。

Problem D

Solved by zerol. 01:19 (+1)

Problem E

Upsolved by kblack.

题意：一堆概率出现的点，求在任意点左下角的点数的期望。

题解：记录不在任意点左下角的概率，每个点相当于对一个矩形乘以 $(1-p)$，扫描线+线段树即可。

Problem F

Solved by ultmaster. 00:37 (+)

Problem G

Solved by kblack. 00:39 (+)

枚举即可，温暖的规律签到。

Problem J

Solved by kblack. 04:05 (+8)

题意：naive 的 hash 函数，naive 的解决方法（往后放），给出结果，求字典序最小的原插入顺序。

题解：很明显的拓扑排序，原题解是线段树优化。也可以考察特殊条件，所有相交的区间合并，包含的区间只会被跳一次，瞎几把搞一搞就好了，注意无解的判断即可。