2012-2013 ACM-ICPC Northeastern European Regional Contest (NEERC 12)
NEERC 12
- 某三题题解[solutions]
- 官方题解[solutions]
Problem A
Solved by oxx1108. 00:34
题意:签到题,消灭星星。给定每次消的个数,构造初始状态。
题解:由于没有限定颜色个数,蛇形放就行。
Problem B
Upsolved by oxx1108.(-16)
垃圾题目毁我青春
题意:求题意比较难懂。(题意巨坑)
给一些物品,每个可以取或者不取,想要不大于$c$的最大物品重量和。
一开始随机有一个A序列(01串),每一位表示物品取还是不取。
每次给一个随机B序列的重量和,随机方式是在A序列上随机修改一位01。
每次有三个选项,可以拿新的B串代替A串,不做任何操作,或者结束操作直接返回(答案就为现在的B串)。
要求操作次数少于1000。
题解:直接先将01串变为全0,然后变为全1,然后就可以计算出每个物品的质量,状压算出最大状态,最后随机到答案。
由于没看到一开始A序列随机死活过不了。
Problem C
Solved by Xiejiadong.02:53(+9)
题意:给每个人分配一个相同的长度,使得每个人可以在自己的区间里面找出互不重叠的区间。
题解:用long double来二分答案,然后暴力枚举分母,找出分数的表示。
需要注意精度问题,wa到自闭。
Problem D
Unsolved.
题意:
题解:
Problem E
Solved by oxx1108.02:29(+1)
题意:给定一些砝码箱,每个砝码箱里有若干个10的次幂的砝码。求能够称出$x$至少需要几个箱子。
题解:从个位开始贪心放,讲所有能取的都扔进一个一个优先队列,每次都取最大的放即可。 忘了考虑1e18,wa了一发。
Problem F
Unsolved.
题意:
题解:
Problem G
Solved by dreamcloud.02:01(+1)
dreamcloud:罚时是不会数位dp的oxx贡献的。
题意:[0,n]中有多少个数满足k进制下,和-k进制下表达一样
题解:转换一下题意,就变成了一个数取k进制之后,$a_m,a_{m-1},……a_3,a_2,a_1,a_0$,要满足$a_m,,……,0,a_2,0,a_0$,即奇数位一定是0,数位dp一下。
Problem H
Solved by dreamcloud.01:34
题意:给你一个字符串s,求它有多少个子序列,满足重构之后是回文串。(重构指的是将子序列中的字符任意交换位置)
题解:子序列重构是回文,其实就是最多只有一个字母出现次数是奇数。利用hash异或和来维护前缀中每个字母出现的次数为奇还是为偶。从前往后扫,要么每个字母都是偶数,要么枚举一个字母出现奇数,只需要看前面该状态有多少个。类似于EOJ七月月赛。
Problem I
Unsolved.
题意:
题解:
Problem J
Solved by Xiejiadong. 03:59(+1)
题意:从0出发,用$a$次$\pm 1$,$b$次$\pm 2$,$c$次$\pm 3$遍历所有的$0$到$a+b+c$点。
题解:先把$c$次$\pm 3$的处理掉。我们通过向右、向左、再向右三部分,把前面的一部分填满,并且最后填的一个的左边已经全部填满,右边全部没有填过
再向右一步一步填,剩下一个$\pm 1$用来在最后改变方向,剩下的$\pm 2$我们用过向右、转弯、向左来填满右边剩下的部分
注意各类情况的处理与细节问题
Problem K
Unsolved.
题意:
题解:
Problem L
Upsolved by Xiejiadong.
题意:给定一个点阵,点阵中本身存在障碍物,现在要求用一个最小的正方形填在没有障碍物的子矩阵中作为障碍,使得无法从$(1,1)$走到$(n,m)$,求这个最小正方形的边长和左上角的坐标。
题解:首先是两个概念,一张点阵中从$(1,1)$到$(n,m)$不再联通的条件是,那个正方形同时切断了图中的左手路径和右手路径
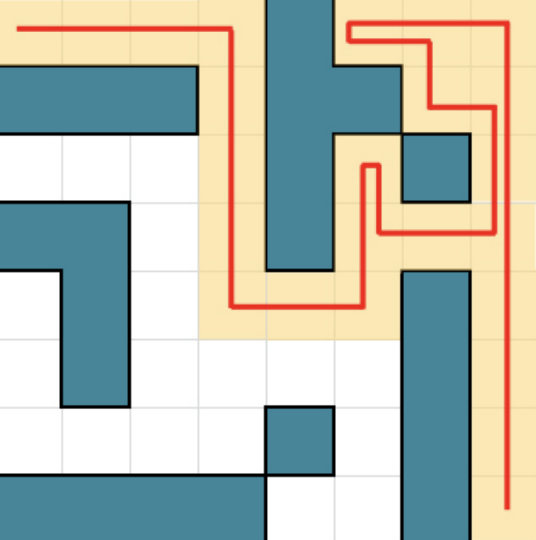
所谓左手路径就是从$(1,1)$开始一直向右,左手一直扶在墙上所走出的路径,如右图:
右手路径的解释正好与之相对应。
走左手路径的方式是:如果前进方向的左边一直有墙,一旦前面碰墙,右转;如果左边没有墙了,左转;如果左边和前面以及右边都有墙,掉头。右手路径的处理方式与之相反。
处理完了路径,我们只需要枚举我们要填正方形的左上角的左边,然后二分正方形的边长,具体二分是:
- 如果该边长所覆盖的区域本身有障碍,缩小边长
- 如果该边长所覆盖的区域没有左手路径或者右手路径,增大边长
这样一来,我们剩下的问题就是怎么$O(1)$的回答当前正方形区域有没有障碍和有没有左右手路径了
对有障碍和左右手路径的坐标分别标记,然后处理一下前缀和,就可以直接查询当前区间里面是否有障碍和左右手路径了