94 人解决，120 人已尝试。
121 份提交通过，共有 399 份提交。
3.5 EMB 奖励。
2703. Class
单点时限: 5.0 sec
内存限制: 256 MB
Dr. Strange is a really strange lecturer. Each lecture he calculates class fullness and if it is small, he decreases all semester grades by one. So the students want to maximize the class fullness.
The class fullness is the minimum of row fullness and column fullness. The column fullness is the maximum number of students in a single column and the row fullness is the maximum number of students in a single row.
For example there are 16 students shown on the left picture (occupied desks are darkened). The row fullness of this arrangement is 5 (the 4-th row) and the column fullness is 3 (the 1-st, the 3-rd, the 5-th or the 6-th columns). So, the class fullness is 3. But if the students rearrange as shown on the right picture then the column fullness will become 4 (the 5-th column), and so the class fullness will also become 4.
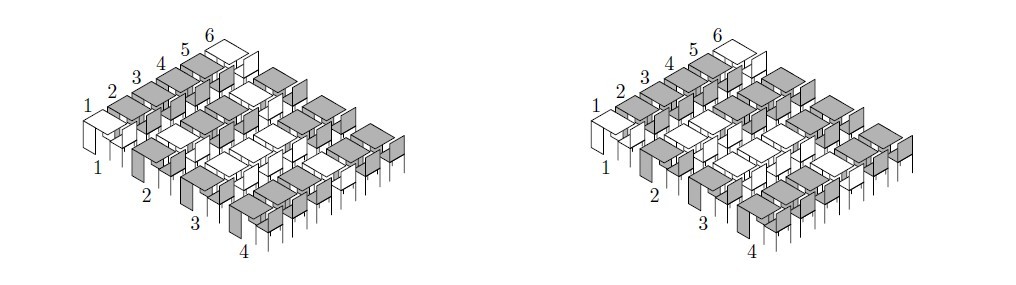
The students of Dr. Strange need to know the arrangement that maximizes class fullness so they ask you to write a program that calculates it for them.
输入格式
The first line of the input file contains three integer numbers: $n$, $r$ and $c$ ― number of students, rows and columns in the class ($1 \le r, c \le 100, 1 \le n \le r \times c$).
输出格式
The first line of the output file must contain a single integer number ― the maximum possible class fullness.
The following $r$ lines must contain the optimal student arrangement. Each line must contain a description of a single row. Row description is a line of $c$ characters either . or #, where . denotes an empty desk, and # denotes an occupied one. If there are multiple optimal arrangements, output any one.
样例
Input
16 4 6
Output
4 .####. #..### #...## ###.##